Định lý virial

Không biết bạn đọc thế nào, tôi viết mấy bài liền về vật lý lượng tử thấy mệt rồi, trong bài này chúng ta quay về thế giới cổ điển quen thuộc. Một định lý quan trọng nhất của vật lý cổ điển, ít khi được dạy trong chương trình phổ thông, là định lý virial, do Clausius tìm ra cuối thế kỷ 19. Ông Clausius cũng chính là người đưa ra khái niệm entropy.

Định lý như sau:

Giả sử ta có một hệ các hạt tương tác với nhau và chuyển động có giới hạn, không hạt nào chạy ra vô cùng (ví dụ như hệ mặt trời). Lúc đó, trung bình của động năng T tỷ lệ với trung bình của một đại lượng Clausius gọi là virial:

$2\langle T\rangle = -\langle \sum_i {\bf r}_i \cdot {\bf F}_i\rangle$

Dấu $\langle \rangle$ ở đây phải hiểu là trung bình theo thời gian. Ở vế phải F_i là lực tác động lên hạt i, và r_i là tọa độ của hạt đó. Ở vế phải ta lấy tổng theo tất cả các hạt trong hệ. Định lý này không khó chứng minh, ví dụ xem ở đây.

Định lý virial có ý nghĩa rõ ràng nhất trong trường hợp lực tương tác giữa các hạt tỷ lệ với một lũy thừa nào đó của khoảng cách. Ví dụ nếu các hạt tương tác với nhau qua lực hấp dấn thì định lý virial nói rằng:

$-2\langle T \rangle = \langle V \rangle$

Ở đây V là thế năng. Ví dụ trong hệ mặt trời, trung bình của thế năng của các thiên thể bằng bằng -2 lần trung bình của động năng. Năng lượng toàn bộ, tức là tổng của động năng và thế năng, bằng âm của trung bình của động năng (hệ mặt trời là hệ liên kết nên năng lượng âm):

$E = T + V = - \langle T\rangle$

Bài tập: mặt trời có khối lượng M=2×10³⁰ kg, bán kính R=7×10⁸ m, cấu tạo từ hydro là chủ yếu. Nhiệt độ trung bình trong lòng mặt trời là khoảng bao nhiêu độ?

This entry was posted in Uncategorized. Bookmark the permalink.

9 responses to “Định lý virial”

Dung Nguyen | June 26, 2010 at 4:07 pm | Reply

Em đã được biết đến định lý Virial, nhưng mà áp dụng nó để tính nhiệt độ mặt trời thì lần đầu tiên em được thấy. Người nghĩ ra cách làm này quả thật là rất thông minh và sáng tạo. Tuy còn có chỗ chưa rõ lắm trong đề bài phần bài tập, là mặt trời cấu tạo từ nguyên tử Hydro hay là từ proton ( hạt nhân nguyên tử hydro ) và electron tự do. Em sẽ thử theo cách suy đoán của em là với nhiệt độ cao thì sẽ là dạng plasma với electron tự do và hạt nhân proton. Và để tính đến nhiệt độ thì coi rằng electron và proton cân bằng nhiệt với nhau. Thế năng hấp dẫn giáo sư đã cho ở bài trước rồi :

$V= - \frac{GM^2}{R}$

Vậy ta có động năng

$K=-V/2=\frac{GM^2}{2R}$

Số hạt electron và số hạt proton cùng bằng

$N=M/m_p$

Dùng công thức động năng cho cả proton và electron theo nhiệt động lực học cổ điển ( coi cả 2 đều là hạt đơn nguyên tử với 3 bậc tự do)

$K_e=K_p=\frac{3{k}_{B}T}{2}$

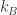với $k_B$ là hằng số Boltzmann và T là nhiệt độ. Ta có :

$K=2N\frac{3{k}_{B}T}{2}$

Từ đó ta có công thức nhiệt độ trung bình của mặt trời:

$T=\frac{2{m_p}GM}{3R{k_B}} =1.54\times 10^7 (Kenvil)$ .

Giáo sư có mê bóng đá không ạ, em tranh thủ giảo lao giữa trận Korea và Uruguay vào thăm blog của giáo sư thì thấy bài có viết mới này.
- damtson | June 27, 2010 at 10:29 am | Reply
  
  Đúng. Chắc bạn cũng hiểu những con số như 2/3, 3/2 trong lời giải của mình là vượt quá độ chính xác của tính toán. Ví dụ trong công thức của thế năng ở trên, V=−GM²/R, ta không biết hằng số đứng đằng trước vì không biết phân bố khối lượng bên trong mặt trời.
  
  Bài 2, cho những người không thờ ơ với tương lai: vài tỷ năm nữa sẽ đến lúc nhiên liệu hydro trong mặt trời bị đốt hết. Sau thời điểm đó, mặt trời sẽ nguội dần đi hay nóng dần lên?
  - Dung Nguyen | June 27, 2010 at 11:55 am |
    
    Câu hỏi thứ 2 này của giáo sư em chỉ dám đoán mò thôi. Vì theo định lý Virial, thì năng lượng của tổng động năng và thế năng là
    
    $E=-=1/2$
    thế nên em nghĩ sau khi đốt hết nhiên liệu, bán kính của khí khối cầu khí Heli ( là kết quả của quá trình đốt Hydro) sẽ giảm để làm giảm thế năng và tổng năng lượng đồng thời cũng lại làm tăng động năng, vì thế nhiệt độ của mặt trời sẽ tăng vì động năng tăng sau quá trình đã hết nhiên liệu Hydro.
    
    Em có một câu hỏi là sau khi mặt trời hết nhiên liệu rồi thì liệu trái đất có thể tồn tại được nữa không nếu bị đốt cháy bởi mặt trời. Lúc đó có lẽ người trên trái đất cũng khó lòng di cư đến các hành tinh trong hệ mặt trời mà phải tìm nơi khác. Nhưng nếu rồi ngôi sao nào cũng sẽ có lúc hết nhiên liệu mặt trời thì rõ ràng sự tồn tại của sự sống là hữ hạn. Nghĩ đến đấy em liên tưởng đến có một định mệnh mà không thể chống lại được.
hoadai | June 27, 2010 at 1:32 pm | Reply

Bài 2 em nghĩ là mặt trời sẽ phìng to ra và đồng thời nguội dần đi.

Lý do là khi gần hết nhiên liệu thì trị tuyệt đối của năng lượng của mặt trời sẽ giảm, do đó theo định lý Virial thì trị tuyệt đối của thế năng cũng giảm. Điều đó dẫn tới mặt trời phìng to ra.

Mà nhiệt độ tỉ lệ nghịch với bán kính (theo công thức cuối cùng trong bài trả lời #1 của bạn Dung Nguyen), nên nhiệt độ sẽ giảm đi.
- Dung Nguyen | June 28, 2010 at 2:33 am | Reply
  
  Thực ra mình cũng biết mặt trời sau khi chết sẽ chuyển thành sao khổng lồ đỏ, nhưng mình nghĩ nó không nằm hoàn toàn trong khuôn khổ định lý Virial, mà phải tính đến sự không đồng nhất của mặt trời, và sự khác nhau giữa các lớp của mặt trời. Mình cho rằng lớp trong của mặt trời gồm các nguyên tố không thể tổng hợp hạt nhân được nữa sẽ co lại và nóng lên.
Pisces | July 17, 2010 at 7:09 pm | Reply

Nhân bài này của anh, em gửi lại 1 thắc mắc “ấm ớ” đã viết bên blog anh Văn. 🙂

Câu hỏi của em là có phải thế giới vật chất có khả năng được chia nhỏ vô hạn, tức là các khám phá về thế giới vi mô ko bao giờ đi đến tận cùng dc, nhưng vẫn đảm bảo sự tồn tại của vật chất vĩ mô ko? Hình dung 1 cách thô sơ như 1 khái niệm trong Toán học, tổng của vô hạn các số trong 1 chuỗi số dương hội tụ lại là 1 số hữu hạn (xác định)?

Nếu đúng như vậy, thì phải chăng có thể hình dung 1 hạt bất kỳ trong vũ trụ hiện nay (proton, notron, electron…) là “tổng” của 1 chuỗi vô hạn (và hội tụ) của các hạt vi mô? Nếu vậy, có phải nhiệm vụ của con người là ko phải tìm ra có những hạt nào, mà là tìm ra “quy luật” tạo thành các hạt đó? Giống như ta ko thể cứ đi tính giá trị của từng thành phần trong chuỗi vô hạn xem nó bằng bao nhiêu, vì tính mãi cũng ko bao giờ đi đến tận cùng dc, mà là tìm công thức biểu diễn các thành phần đó?
Bởi vì nếu ko phải là vô hạn, giả sử có 1 hạt bé nhất, thì lại có 1 câu hỏi đặt ra là cái hạt bé nhất đó cấu tạo từ cái gì? 🙂

Em nghĩ 1 cách thô sơ vậy thôi, chứ ko chắc đúng về hiện tượng Vật lý. 🙂
Dung Nguyen | July 24, 2010 at 5:24 pm | Reply

Nếu có chút thời gian, xin giáo sư cho ý kiến về bài báo của tiến sỹ Verlinde cho rằng lực hấp dẫn không tồn tại. Em xin cảm ơn.
- damtson | August 16, 2010 at 6:43 am | Reply
  
  Rất tiếc là tôi chưa đọc chi tiết, chưa có ý kiến gì được.
damtson | August 16, 2010 at 6:37 am | Reply

Lời giải của câu đố: lúc mặt trời đốt hết hydro, nó sẽ bị mất năng lượng do bức xạ ra ngoài vũ trụ. Năng lượng giảm đi dẫn đến bán kính tăng giảm đi, và nhiệt độ tăng lên, theo định lý virial.