Lùn trắng

Hôm nay ta sẽ nói đến một ứng dụng của nguyên lý bất định vào vật lý thiên văn. Đó là ứng dụng vào sao “lùn trắng”.

Sao lùn trắng là những sao đã tàn. Nhiên liệu hạt nhân đã đốt hết, những sao này nguội dần đi do mất năng lượng vào trong chân không. Nhưng chúng còn phát sáng trong một thời gian, do đó người ta gọi là “trắng”, còn chữ “lùn” là do kích thước của chúng rất nhỏ so với các ngôi sao bình thường. Về thành phần thì chúng thường là carbon hoặc ôxi, những sao nhẹ thì là hêli. Những sao này là những hệ rất đơn giản, về mặt vật lý chỉ có lực hấp dẫn cân bằng với áp suất. Trong bài này chúng ta sẽ tìm hệ thức giữa khối lượng và bán kính của các sao lùn trắng này.

Giả sứ khối lượng của sao là M. Những nguyên tử các nguyên tố nhẹ như hêli, carbon, ôxi đều tương đối giống nhau về thành phần: cứ 1 electron thì có 1 proton và 1 neutron. Nhắc lại: khối lượng của proton m_p và neutron m_n gần như bằng nhau, m_p ≈ m_n ∼ 1.67×10^-24 g, lớn hơn nhiều khối lượng electron. Như vậy số lượng electron trong một ngôi sao khối lượng M là N=M/2m_p, và ngôi sao cũng chứa đúng từng đấy proton, và đúng từng đấy neutron.

Nhiệm vụ của ta là tìm bán kính R của ngôi sao này. Có một bán kính tối ưu là vì như sau. Nếu R quá lớn, ngôi sao sẽ co lại do lực hấp dẫn. Nhưng nếu R quá nhỏ, thì mỗi electron có một khoảng không gian quá hạn chế, theo nguyên lý bất định nó sẽ có chuyển động lượng tử, và vận tốc của chuyển động này càng lớn khi R càng nhỏ, do đó áp suất bên trong của ngôi sao sẽ tăng lên khi R giảm đi. Bán kính của lùn trắng được xác định bởi sự cân bằng giữa lực hấp dẫn và áp suất do chuyển động lượng tử của electrons.

Thay vì xét phương trình cân bằng lực, ta sẽ tìm cực tiểu của năng lượng. Thế năng do tương tác hấp dẫn là

$U=-\displaystyle{\frac{GM^2}R}$

Bây giờ ta chuyển sang tìm động năng. Thể tích của sao là R³, nên mỗi electron bị nén trong một thể tích bằng R³/N=R³m_p/M. Ta có thể hình dung mỗi electron bị giới hạn chỉ được chuyển động trong một hộp có kích thước là l=R(m_p/M)^1/3.

Bây giờ ta nhớ lại nguyên lý bất định: mỗi electron sẽ có xung lượng ít nhất bằng p=ħ/l, và năng lượng ε=p²/(2m_e)~ħ²/(m_el²). Như thế thì động năng của tất cả các điện tử trong ngôi sao sẽ là

K=Nε

Những bước tiếp theo tôi sẽ để cho các bạn tự làm. Kết quả của việc cực tiểu hóa năng lượng (=động năng + thế năng) sẽ là mối liên hệ sau đây giữa bán kính và khối lượng:

MR³=constant

Các bạn có thể tham khảo thêm số liệu quan sát thiên văn ở bài này để xem xem hệ thức trên có đúng không.

This entry was posted in Uncategorized. Bookmark the permalink.

10 responses to “Lùn trắng”

Dung Nguyen | June 19, 2010 at 6:46 pm | Reply

Kết quả sau phép tính đơn giản là

$MR^3=\frac{\hbar^6}{{m_e}^3{m_p}^5G^3}\approx 4.66 \times 10^{50}$ .

Em thử lại cho Sirius B thì ra kết quả là:
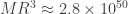
$MR^3 \approx 2.8 \times 10^{50}$

Nhưng với công thức ước lượng của xung lượng, thì tính giá trị vận tốc của electron theo phép tính cổ điển $v=p/m_e$ thì vận tốc của electron cỡ $2.4 \times 10^8 m/s$ như vậy là gần vận tốc ánh sáng, em nghĩ cần phải tính thêm hiệu ứng tương đối vào nữa. Và công thức tính thế năng hấp dẫn em đoán rằng là cho vật khối lượng đồng nhất ( Em chưa thử tính lại). Nhưng trong một ngôi sao thì khối lượng chắc là sẽ không đồng nhất mà giảm dần từ trong ra ngoài ( Em đoán thế do bên trong áp suất phải lớn hơn nên nén chặt hơn).

Em mong giáo sư sẽ sớm có một blog nói về sự liên quan của phép đo trong cơ học lượng tử và nguyên lý bất định.

Xin cảm ơn giáo sư vì thời gian giải trí thú vị với bài viết mới.
- Dung Nguyen | June 19, 2010 at 6:49 pm | Reply
  
  Xin lỗi giáo sư, em lại quên đơn vị trong 2 công thức đầu tiên, em dùng đơn vị SI, là $kgm^3$ .
- damtson | June 22, 2010 at 4:27 am | Reply
  
  Đúng là những tính toán trình bày trong bài chỉ đúng trong trường hợp vận tốc điện tử nhỏ hơn nhiều vận tốc ánh sáng. Bạn có thể tìm hiểu vấn đề sau: liệu các công thức trong bài thay đổi thế nào nếu các điện tử là ultra-relativistic (p>>mc, lúc đó liên hệ giữa năng lượng và xung lượng là ε=pc).
  - Dung Nguyen | June 22, 2010 at 7:50 am |
    
    Chà, lúc chưa tính thử thì em nghĩ la chắc cũng sẽ có một công thức $MR^n=constant$ , nhưng sau khi thử tính thì thấy kết quả tự nhiên thú vị hơn nhiều. Cỡ của động năng là
    
    $K=\frac{c\hbar}{{m_p}^{4/3}}\times \frac{M^{4/3}}{R}$
    
    như vậy là cả thế năng và động năng có cùng bậc đối với R là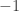 $-1$ . Xét công thức tổng năng lượng là
    
    $E= -\frac{GM^2}{R}+\frac{c\hbar}{{m_p}^{4/3}}\times \frac{M^{4/3}}{R}$
    
    Dẫn đến một giới hạn của khối lượng :
    
    $M_0=\frac{c^{3/2}\hbar^{3/2}}{G^{3/2}{m_p}^2}$ .
    
    Nếu $M>M_0$ thì R sẽ tiến tới 0, white draft sẽ collapse.
    
    Tưởng như sẽ có một giới hạn nữa khi
    $M M_0$ , sẽ xảy ra giới hạn ultra-relativity và white draft sẽ collapse, nhưng cái kết quả R tiến tới 0 có vẻ không được physics cho lắm. Em nghĩ rằng với một điều kiện nào đó thì sẽ dẫn đến black hole (cái này em chỉ đoán mò thôi vì em nghĩ đến mật độ khối lượng lớn khi collapse) hoặc trong lúc collapse sẽ có điều gì đó xảy ra chứ không thể để R tiến tới 0 được.
    
    Thêm nữa là em tinh ra khối lượng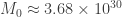 $M_0 \approx 3.68\times 10^{30}$ nó chỉ khoảng 1.8 lần khối lượng mặt trời, em không biết như thế liệu có nhỏ quá không.
    
    Xin giáo sư xóa hộ em cái comment phía trên, em lại bị lỗi đánh máy rồi. Em xin cảm ơn.
  - Dung Nguyen | June 22, 2010 at 1:16 pm |
    
    Em còn một đoạn nữa chứng minh rằng giới hạn M> mc nên không thể xảy ra. Nhưng em thử vài lần mà không làm sao hiện ra trên wordpress được nên mới xuất hiện nhiều bài post, làm mất thời gian của giáo sư. Nhưng câu hỏi quả thật rất thú vị.
  - damtson | June 26, 2010 at 5:13 am |
    
    Đây chính là giới hạn Chandrasekhar: sao lùn trắng không thể có khối lượng lớn hơn giới hạn này. Tính toán chính xác hơn cho thấy giới hạn này là 1.46 khối lượng mặt trời. Những sao có khối lượng lớn hơn phải là sao neutron, hoặc lỗ đen. Chandrasekhar tìm ra giới hạn này năm 1930, trong khi đi tàu thủy từ Ấn độ sang Anh để học PhD.
thichhoctoan | June 19, 2010 at 9:30 pm | Reply

Tức là áp suất không khí cũng có nguồn gốc từ nguyên lý bất định, có đúng không ạ ?
- damtson | June 21, 2010 at 12:04 pm | Reply
  
  Không, không khí thì nhiệt độ cao quá để các hiệu ứng lượng tử đóng vai trò đáng kể. Nếu ta lấy không khí rồi coi x là khoảng cách giữa các phân tử, p là xung lượng của chúng do chuyển động nhiệt, và tính xp thì thấy nó lớn hơn nhiều so với hằng số Planck ħ.
- damtson | June 26, 2010 at 7:29 am | Reply
  
  Nói tiếp về áp suất của không khí. Áp suất P của một chất khí đại khái bằng tích của mật độ n (bao nhiêu phân tử trong một cm³) và năng lượng trung bình của mối phân tử ε. Mật độ càng cao thì áp suất càng cao, và năng lượng của mỗi phân tử càng cao thì áp suất càng cao. Trong trường hợp không khí, các hiệu ứng lượng tử có thể bỏ qua, và năng lượng của mỗi phân tử tý lệ thuận với nhiệt độ: ε~kT, k là hằng số Boltzmann. Do đó P ~ nkT. Trong sao lùn trắng thì năng lường của mỗi điện tử có nguồn gốc từ nguyên lý bất định, đóng góp của nhiệt độ không đáng kể.
BB | June 23, 2010 at 3:36 pm | Reply

Cảm ơn anh Sơn. Cách tư duy thật sáng sủa làm em thấy nhớ Vật lý quá. Còn nhớ có lần thầy Đàm Trung Đồn dạy cách tìm hằng số Planck xuất phát từ những luận điểm khá quen thuộc 🙂