Lúc còn bé tôi có lúc đã từng say sưa đọc hai cuốn sách “Ba ngày ở nước tí hon” và “Người mặt nạ đen ở nước An-giép”. Sách dịch từ tiếng Nga, tên tác giả là Levshin, gần đây đã được tái bản lại ở Việt Nam. Hai cuốn sách mô tả các cuộc phiêu lưu của 3 em học sinh vào một thế giới diệu kỳ, ở đó các con số là những sinh vật sống động hẳn hoi. Các em làm quen dần với những loại số khác nhau, đầu tiên là số nguyên dương, sau đến số thập phân, rồi số âm, số ảo, số phức. Tôi còn nhớ chuyện các em gặp đơn vị ảo i, nó rất bất mãn là bị người ta gọi là “ảo”, trong khi nó là một con số rất cần thiết.
Những người đầu tiên nghiên cứu vật lý lượng tử cũng giống như các nhà thám hiểm đi đến một thế giới mới. Họ thấy thế giới này lạ đến mức các loại con số trước đây người ta vẫn dùng không còn đủ để đáp ứng nhu cầu nữa, nên họ phải nghĩ ra các loại số mới.
Ta nhớ lại là những ý tưởng đầu tiên về cơ học lượng tử đến với Heisenberg khi ông ta đi nghỉ ở một hòn đảo. 9-10 ngày sống trên hòn đảo không có một ngọn cỏ nào làm cho bệnh dị ứng của ông ta qua đi, và khi về ông ta viết những lại những tính toán của mình thành một bài báo — bài đầu tiên của môn cơ học lượng tử mới. Bài báo này hoàn toàn không dễ đọc. Max Born (đừng nhầm với Niels Bohr), cùng với học trò của mình là Jordan đọc bài báo này và đi đến kết luận rằng nội dung của nó có thể được kết tinh lại bằng một công thức như sau:
Nhắc lại ở đây: là tọa độ của một hạt (để cho đơn giản ta cho hạt chỉ chạy trên một đường thẳng),
là xung lượng (tích của khối lượng và vận tốc,
),
là hằng số Planck, và
là đơn vị ảo,
.
Bạn đọc chắc thấy công thức này rất lạ. Ta biết rằng 3×5=15, mà 5×3 cũng bằng 15: khi ta đổi hai thừa số của một phép nhân, thì tích không thay đổi. Đây tính giao hoán của phép nhân và ta coi nó là hiển nhiên, nhiều khi không nghĩ tới nó nữa. Nhưng công thức trên kia của Born và Jordan thì lại cho thấy rằng không bằng
, nghĩa là phép nhân không còn tính giao hoán nữa. Như vậy tọa độ
và xung lượng
không thể là những số thường, mà phải là những số lạ. Bây giờ người ta gọi những “số lạ” này bằng một thuật ngữ toán học khá dài “toán tử tuyến tính trong không gian Hilbert”, nhưng tôi thích cái tên ngắn gọn do Dirac đặt ra hơn: số q (q-numbers). Chữ q ở trong cái tên này là viết tắt của quantum, tức là lượng tử. Những số thường (bao gồm số thực, số phức) thì Dỉrac gọi là số c (c-numbers), c là viết tắt của chữ classical (cổ điển). Trong thế giới lượng tử, phép nhân không còn tính giao hoán nữa.
Trong đoạn tiếp theo chúng ta sẽ làm quen với khái niệm số q này. Đoạn dưới đây cần một số kiến thức về toán sơ cấp, ví dụ khái niệm số phức. Bạn đọc nào không quan tâm lắm đến toán có thể nhảy xuống Kết luận và chờ đọc tiếp phần tiếp theo của loạt bài này. Những điều viết dưới đây mang tính chất giới thiệu, không nhằm đạt đến sự chặt chẽ về toán học.
Các phép tính với số q
Để phân biệt số q với số c, ta sẽ để một dấu mũ lên chữ cái ký hiệu các số q: ,
, còn các số c thì ta không để dấu mũ lên. Công thức mà Born và Jordan kết tinh lại từ bài báo của Heisenberg như vậy ta phải viết là
Ta sẽ gọi phương trình này là hệ thức Born-Jordan. Ngược lại, các số c bao giờ cũng giao hoán với nhau:
Ta cũng có thể lấy một số c nhân với một số q. Trong trường hợp này, phép nhân cũng mang tính giao hoán:
Có thể coi số c là một trường hợp riêng của các số q: các số c giao hoán với tất cả các số khác.
Phép nhân các số q vẫn có tính kết hợp:
như phép nhân các số c bình thường.
Cũng như với các số bình thường, có khái niệm số q thực và số q phức. Tọa độ và xung lượng là những thứ đo được, nên và
là số q thực. Nhưng ví dụ
là số q phức. Ta cũng có khái niệm số q phức liên hợp. Số phức liên hợp của
là
. Để cho tiện, số phức liên hợp của
ta ký hiệu là
, thêm chữ thập ở đăng sau.
Một điều cần chú ý là nếu ta lấy hai số q thực nhân với nhau thì kết quả chưa chắc đã là số q thực, mà nói chung là số q phức. Ta có thể thấy điều này ở hệ thức Born-Jordan ở trên: nếu và
đều thực, thì hiệu của chúng không thể nào là số ảo. Nhưng ta có thể quy định là nếu ta đổi chỗ hai thừa số thì ta nhận được số q phức liên hợp của tích trước khi đổi:
Điều kiện này không mâu thuẫn với hệ thức Born-Jordan, vì hiệu của và
sẽ là hiệu của hai số phức liên hợp, và là số thuần ảo.
Bạn đọc có thể tự kiểm tra là nếu và
là hai số q phức,
,
trong đó các số
,
,
,
là các số q thực, thì
Các bạn biết đại số tuyến tính có thể thấy các tính chất của phép nhân của số q giống tính chất của nhân ma trận. Bài tập: chứng minh rằng các số q và
không thể là các ma trận hữu hạn chiều.
Kết luận
Như vậy ta đã thấy trong thế giới lượng tử các đại lượng vật lý thông thường như tọa độ, vận tốc, xung lượng đều là các số q. Nhưng tất cả các thiết bị đo đạc của chúng ta không có máy nào cho ra số q, chỉ toàn cho ra số c thôi. Đằng sau sự xung khắc giữa số q và số c là những điểm mấu chốt của cơ học lượng tử, những điểm vẫn còn gây ra các cuộc tranh cãi vô tận về triết học. Nếu có dịp ta sẽ bàn tiếp về vấn đề này, và ta sẽ thấy tính không giao hoán của các số q liên quan đến nguyên lý bất định như thế nào.

khi học cơ lượng tử em thấy một số người rất khó chấp nhận tính giao hoán đó tức là AB≠BA. nên khi dạy các bạn nhỏ em lấy ví dụ là đánh răng gọi là toán tử A, và rửa mặt là toán tử B. Khi đó AB sẽ là đánh răng + rửa mặt= mặt sạch sẽ.
tuy nhiên, nếu như BA tức là rửa mặt + đánh răng = mặt …
như vậy từ cuộc sống cho thấy cơ học lượng tử cũng khá gần gũi đấy chứ
Rất hay! Anh mới chỉ nghĩ ra dùng khối Rubik để mô tả tính không giao hoán của các phép quay thôi.
Thưa giáo sư em có 2 câu hỏi.
Câu hỏi thứ nhất là từ việc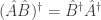 thì có thể khẳng định rằng biểu thức giao hoán tử của hai số q thực luôn cho một số q thuần phức hay không.
thì có thể khẳng định rằng biểu thức giao hoán tử của hai số q thực luôn cho một số q thuần phức hay không.
Câu hỏi thứ 2 là đồng nhất thức Jacobi ( Jacobi identity) có phải là hệ quả trực tiếp từ việc bảo tồn tính kết hợp của số q phức hay không. Và xin giáo sư cho thêm một số ý nghĩa của đồng nhất thức Jacobi trong vật lý.
Phần bài tập có lẽ là lấy vết (Trace) của cả 2 vế hệ thức giao hoán Born Jordan. Nếu p và x là hữu hạn chiều thì vế trái bằng 0 còn vế phải thì khác 0.
1. Nếu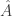 và
và 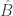 là hai toán tử Hermitian, thì
là hai toán tử Hermitian, thì ![[\hat A,\, \hat B]](https://s0.wp.com/latex.php?latex=%5B%5Chat+A%2C%5C%2C+%5Chat+B%5D&bg=ffffff&fg=333333&s=0&c=20201002) là anti-Hermitian (khai triển
là anti-Hermitian (khai triển ![[\hat A,\, \hat B]^\dagger](https://s0.wp.com/latex.php?latex=%5B%5Chat+A%2C%5C%2C+%5Chat+B%5D%5E%5Cdagger&bg=ffffff&fg=333333&s=0&c=20201002) ra là xong).
ra là xong).
2. Nếu không có tính kết hợp thì chắc không thể có đồng nhất thức Jacobi. Trong vật lý đồng nhất thức này dẫn đến việc các đại lượng bảo toàn lập nên một đại số Lie khép kín: nếu![[\hat H,\, \hat A]=[\hat H,\, \hat B]=0](https://s0.wp.com/latex.php?latex=%5B%5Chat+H%2C%5C%2C+%5Chat+A%5D%3D%5B%5Chat+H%2C%5C%2C+%5Chat+B%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) thì
thì ![[\hat H,\, [\hat A,\, \hat B]]=0](https://s0.wp.com/latex.php?latex=%5B%5Chat+H%2C%5C%2C+%5B%5Chat+A%2C%5C%2C+%5Chat+B%5D%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) .
.
3. Bài tập bạn giải rất đúng!
Cảm ơn giáo sư đã trả lời câu hỏi của em. Sau khi đọc lại bài viết của giáo sư, em còn thêm một số câu hỏi khác.
Trong bài viết giáo sư liên hệ giữa q số và toán tử. Vậy vai trò của hàm sóng ở đây là gì?
Ta có thể coi c số cũng là q số nhưng trong một hệ chỉ tồn tại 1 vector trạng thái, nghĩa là c số là ma trận 1×1, ví dụ như chỉ xét một tập hợp các toán tử giao hoán với nhau và cùng nhận 1 vector trạng thái làm vector riêng không? ( Câu hỏi này có lẽ là ngớ ngẩn)
Câu hỏi tiếp theo của em là có một định lý nào nói rằng bất cứ loại số nào (ví dụ là x-số) mà bảo toàn tính kết hợp của phép nhân thì cũng có thể biểu diễn bằng ma trận và phép nhân cũng tương ứng với phép nhân ma trận không? Em thử chứng minh cho tập hợp số là hữu hạn với phép nhân có tính khép kín thấy không quá khó. Nhưng trong trường hợp tập số có vô hạn phần tử thì em không rõ có thể làm được hay không.
Xin cảm ơn giáo sư.
Toán tử tác động trong một không gian, biến một véctơ thành một véctơ khác. Hàm sóng là một véctơ. Số c thì là hằng số nhân với toán tử đơn vị (toán tử biến một véctơ bất kỳ thành chính nó). Còn câu hỏi cuối cùng thì có lẽ nó liên quan đến lý thuyết nhóm và biểu diễn của nhóm, tôi không biết câu trả lời chính xác. Em thử xem các sách về lý thuyết nhóm xem có nói gì không.
Cám ơn giáo sư đã trả lời câu hỏi trên của em.
Thưa giáo sư, em tiếp tục có thêm câu hỏi và cũng không biết có phải là câu hỏi cuối cùng hay không. Em xin lỗi nếu làm mất thời gian của giáo sư.
Khi giáo sư viết là các đại lượng vật lý trong cơ học lượng tử là q số, nhưng trong các phép đo thì chỉ cho chúng ta c số. Mà đại số của q số và c số là khác nhau. Thế nên không thể có một đẳng cấu giữa q số và c số. Như vậy có thể nói rằng mọi phép đo đều không thể cho ta đầy đủ thông tin về q số hay không?
Cái này tôi dự kiến sẽ là chủ đề của một bài trong tương lai!
thưa giáo sư! Em rất mong muốn được tìm hiểu sâu về vật lý lý thuyết. Nhưng em chưa biết là cần phải học những bộ môn toán nào. Mong giáo sư chỉ dẫn.
Ít nhất là cần: giải tích, đại số tuyến tính, hình học giải tích, phương trình vi phân, lý thuyết hàm biến phức, phương trình đạo hàm riêng. Em có thể tham khảo quyển Arfken, Weber, Mathematical Methods for Physicists để xem phải học những gì.
Giáo sư Gerald ‘t Hooft có một trang này có thể trả lời được câu hỏi của em: How to become a good theoretical physicist.
Thưa giáo sư, e là một người đam mê tìm hiểu kiến thức, và hiện tại kiến thức toán học của em chỉ là đến hết cấp 3 (trước e học trường chuyên KHTN), lên ĐH em không theo ngành toán. Vậy giờ e muốn tìm hiểu cơ học lượng tử thì nên bắt đầu tìm hiều từ đâu và những tài liệu nào e nên tham khảo? Mong giáo sư giúp đỡ. Cảm ơn ạ!