Theo ý kiến của tôi, cơ học lượng tử là một thành tựu văn hoá mang tính phổ quát của nhân loại. Tôi vẫn nhớ lần đầu tiên mình thực sự hiểu được cơ học lượng tử là lúc tôi học năm thứ 3 đại học. Sau đó trong một vài ngày, tôi đi ngoài đường với trạng thái lâng lâng, nhìn những khuôn mặt của những người đi trên đường và nghĩ: những con người kia phần lớn là những người bất hạnh, vì họ cũng như mình vài ngày trước đây không hiểu gì về bản chất lượng tử của thế giới. Cảm giác đó đã qua từ lâu, nhưng tôi nghĩ trong tương lai gần, nếu không phải là ngay bây giờ, một con người được giáo dục toàn diện phải biết những khái niệm cơ bản của cơ học lượng tử, cũng như ai cũng biết đến ba định luật của Newton, hay nguồn gốc phân tử của tính di truyền. Đó là vì không biết các định luật lượng tử thì khó thưởng thức được một phần cái Đẹp của thế giới quanh ta, cái đẹp ở mức nguyên tử.
Đế hiểu sâu, có hệ thống, môn cơ học lượng tử, ta cần một số kiến thức nhất định về toán và vật lý, vượt quá chương trình toán và vật lý phổ thông. Tuy nhiên theo tôi trở ngại lớn nhất để hiểu cơ học lượng tử là trực giác của con người, cái được gọt dũa qua hàng triệu năm tiến hóa. Ta không cần phải biết định luật bảo toàn năng lượng và xung lượng để đoán được rằng khi một hòn bi nhẹ chuyển động và va vào một hòn bi nặng đang đứng yên, thì hòn bi nhẹ sẽ bị bật ngược trở lại, nhưng khi một hòn bi nặng va vào một hòn bi nhẹ đang đứng yên thì hòn bi nặng vẫn tiếp tục tiến lên phía trước như không có chuyện gì xảy ra. Những cảm nhận trên đều là do kinh nghiệm trong cuộc sống hàng ngày, nếu không nói đến việc là nhiều người trong số chúng ta lúc còn bé đã từng chơi bi. Vấn đề của cơ học lượng tử là ta ít có kinh nghiệm với thế giới vi mô — ít ai có dịp chơi với những hòn bi kích thước chỉ bằng một nguyên tử — và chính điều này làm cho các hiện tượng lượng tử trở nên rất khó tiếp thu khi mới làm quen. Nhưng rất may, các nguyên lý của cơ học lượng tử có thể hiểu được, ít nhất là ở mức định tính và nhiều khi ở mức bán định lượng, chỉ cần dùng kiến thức toán và vật lý phổ thông.
Một chút lịch sử
Người đầu tiên tìm ra cơ học lượng tử là Heisenberg. Lúc đó ông ta mới 23 tuổi, đang phải đi nghỉ ở một hòn đảo để chữa dị ứng. Gần như đồng thời, Schrödinger, 38 tuổi, tìm ra cơ học lượng tử theo phương pháp của mình sau khi đi an dưỡng ở một nhà nghỉ trên núi với một người phụ nữ bí ẩn, cho đến nay không ai biết tên. Nếu là họa sĩ, tôi sẽ vẽ một bức tranh mang tên “Bình minh của cơ học lượng tử” mô tả một sự kiện có thật: Heisenberg, qua một đêm tính toán căng thẳng và đã biết rằng lý thuyết của mình là đúng, leo lên một hòn đá nhô ra biển để đón mặt trời lên. Hai phương pháp tiếp cận của Heisenberg va Schrödinger rất khác nhau, nhưng tương đương với nhau. Sau đó năm 1941 Feynman tìm ra một cách phát biểu thứ ba cho cơ học lượng tử.
Trong khuôn khổ bài này, tôi chỉ nói đến nguyên lý bất định của Heisenberg.
Những ai đã học vật lý chắc còn nhớ khái niệm “chất điểm”. Ta tưởng tượng ra một điểm, không có cấu trúc, mang một khối lượng nhất định. Các hạt cơ bản, ví dụ như electron (điện tử), có thể coi là chất điểm: chúng không có cấu trúc gì cả.
Trong cơ học cổ điển, trạng thái của chất điểm bao gồm vị trí của nó, và vận tốc của nó. Trong vật lý có một khái niệm rất tiện dụng là xung lượng. Xung lượng của chất điểm là tích của khối lương và vận tốc: . Vận tốc của một hạt được đo bằng cm/s. Xung lượng đo bằng g cm/s. Động năng của một hạt khối lượng
chuyển động với vận tốc
là
, hoặc ta có thế viết là
.
Trong cơ học cổ điển, tọa độ và xung lượng của một hạt có thể được xác định với một độ chính xác tùy ý. Nhưng trong cơ học lượng tử thì không phải như vậy. Nếu tọa độ dược xác định rất chính xác thì xung lượng không thể xác định chính xác được, và ngược lai. Trên mức độ toán học hơn một chút, nguyên lý bất định của Heisenberg là
trong đó là độ bất định của tọa độ,
là độ bất định của xung lượng, và
(chữ h có gạch ngang ở trên) là hằng số Planck, một hằng số cơ bản của tự nhiên. Giá trị của hằng số này là
=1.054×10-27 g cm2/s
Bản chất của nguyên lý bất định là như thế nào? Nếu ta tóm một con chuột, nó sẽ giãy giụa để chạy ra khỏi tay ta. Ta cứ tưởng tượng vạn vật trong tự nhiên đều như vậy. Nếu ta định “tóm” một vật lại, không cho vị trí của nó xê dịch quá một kích thước bằng , nó sẽ không thể ngồi yên trong đó. Nghĩa là hạt đó sẽ có một xung lượng ít nhất cỡ
, tức là vận tốc ít nhất cỡ
. Chuyển động này được gọi là chuyển động lượng tử.
Bạn đọc đến đây có thể bảo: làm gì có chuyện đó! Nếu tôi có một hòn đá, nếu tay tôi không run, tôi có thể giữ chặt cho nó không cựa cậy được, làm gì có chuyện nó giãy giụa như con chuột! Nhưng thực ra, hòn đá của bạn vẫn cựa cậy, chỉ có điều rất yếu thôi. Đó là do hằng số Planck rất nhỏ. Ta giả sử hòn đá của bạn nặng 100 g, và bạn giữ nó không cho nó cựa cậy quá giới hạn 1 micrômét. Theo công thức của nguyên lý bất định thì hòn đá sẽ cựa cậy với vận tốc là 10-25 cm/s — một vận tốc quá nhỏ để ta có thể cảm thấy được.
Thế nhưng với những hạt rất nhỏ thì hiệu ứng của nguyên lý bất định có thể cảm thấy được. Nếu thay vì hòn đá ta lấy một nguyên tử hyđrô có khối lượng cỡ 10-24 g thì vấn đề khác hẳn rồi. Lúc này tốc độ “cựa cậy” của nguyên tử sẽ là 10 cm/s — một tốc độ ta có thể tưởng tượng được! Thay nguyên tử bằng một hạt điện tử có khối lượng cỡ 10-27 g thì tốc độ này lên tới 100 m/s. Nguyên lý bất định của Heisenberg nói rằng không có cách này giảm tốc độ này xuống bằng không: chuyển động lượng tử là tính chất cố hữu của các vật.
Tại sao điện tử không rơi vào trong hạt nhân
Theo mẫu nguyên tử của Bohr, điện tử quay xung quanh hạt nhân, giống như những hành tinh quay xung quanh mặt trời. Ta có thể hỏi là: tại sao điện tử không rơi vào trong hạt nhân? Nhớ lại là lực giữa hạt nhân và điện tử là lực hút. Nếu điện tử có thể nằm gọn trong hạt nhân, thay vì quay xung quanh hạt nhân, thì thế năng của nó giảm đi nhiều. Nếu ta có thể “ấn” điện tử vào trong hạt nhân thì ta sẽ giải phóng ra một năng lượng khổng lồ.
Nguyên lý bất định của Heisenberg giải thích tại sao điều này không thể xảy ra được. Đó là do nếu ta muốn giam điện tử vào trong một không gian chật hẹp như hạt nhân thì nó sẽ vùng vẫy chạy ở trong đó với một xung lượng rất lớn. Bạn có thể dùng công thức trên và tính ra là vận tốc của điện tử đạt đến tốc độ ánh sáng trước khi ta có thể cầm tù nó trong bán kính của hạt nhân (bằng khoảng 10-13 cm). Như thế thì “lợi bất cập hại”: ta được lợi về thế năng khi cho điện tử vào gần hạt nhân, thì lại thiệt vì bây giờ động năng của nó quá lớn.
Như vậy trong một nguyên tứ, có một khoảng cách tối ưu giữa các điện tử và hạt nhân. Ta sẽ đánh giá khoảng cách này cho nguyên tử đơn giản nhất là nguyên tử hydro, bao gồm một hạt nhân và một điện tử. Đoạn tiếp dưới đây có sử dụng một chút toán học và vật lý. Ký hiệu khoảng cách giữa điện tử và hạt nhân là , lúc đó:
thế năng của hạt sẽ là: , trong đó
là điện tích của electron;
=4.8×10-10 g1/2 cm3/2 s-1.
động năng của hạt sẽ là: , nhưng xung lượng
, nên động năng là
. Khối lượng của điện tử
=9.1×10-28 g.
Năng lượng của hạt là tổng của động năng và thế năng
.
Khảo sát hàm số này, ta thấy nó có cực tiểu ở:
Đây chính là bán kính Bohr của nguyên tử hydro. Giá trị số của đại lượng này là 0.05 nanômét. Kích thước các nguyên tử của các nguyên tố khác đều cỡ 0.1 nanômét cả. Điều này giải thích tại sao khối lượng riêng của tất cả các chất rắn và lỏng đều loanh quanh ở 1–10 g/cm3 cả, không có chất nào khối lượng riêng lên tới 100 g/cm3: trong chất lỏng và chất rắn các nguyên tử đã chạm vào nhau rồi, nếu muốn tăng mật độ lên thì ta phải có một áp suất rất lớn.
Trong một bài viết sau, ta sẽ ứng dụng nguyên lý bất định này để tìm hiểu một loại sao lạ, gọi là sao lùn trắng, chính là nơi vật chất bị nén lại với áp suất khổng lồ.
Bài tập:
Hạt neutron, khối lượng 1.7×10-24 g, nằm trong trọng trường của trái đất. Dưới mặt đất, ở độ cao =0, ta để một cái “gương neutron”, làm bằng chất liệu không cho neutron (năng lượng thấp) đi qua. Neutron bây giờ bị bắt buộc phải ở phía trên gương. Do nguyên lý bất định, neutron không thể nằm chính xác ở độ cao bằng không, mà có một chuyển động lượng tử loanh quanh một độ cao nhất định. Đánh giá độ cao này. Tài liệu tham khảo: hep-ph/0306198

Em cũng cảm thấy mình bất hạnh anh Sơn ạ. Nhưng em vẫn không hiểu cái gì khiến cho electron dao động như vậy, có liên quan gì đến vũ trụ giãn nở hay không.
Hình như entropy tăng thì chuyển động của electroc cũng tăng. Đúng không nhỉ? Lâu quá quên hết rồi.
1.-Không liên quan gì đến vũ trụ giãn nở. 2-Entropy là tính chất thống kê, nói chung chỉ dùng để mô tả các hệ nhiều hạt, không dùng được cho 1 electron. Có thời gian tôi sẽ viết thêm về 2 vấn đề này, nhưng phải từ từ.
Anh Sơn viết hay quá. Hy vọng sẽ được đọc nhiều hơn nữa những bài viết ủa anh.
Em mê vật lý lắm, nhưng không đủ tài năng theo được ngành này. hu hu. Nhưng vẫn ham đọc những bài viết về vật lý lắm lắm. Tiếc là giờ chỉ đọc được những bài mang tính giới thiệu hoặc phổ biến kiến thức thôi.
Bài thơ tình lượng tử
=====================
Nguyễn Hữu Viện
Làm sao mô hình hóa những con
xúc xắc tứ lục đỏ đen khi
Thượng đế không chịu chơi trò may
rủi? Như quần chúng ngày đêm mơ
tổ hợp những con số nhảy múa
mơ mộng bàn đèn. Giữa Thiên niên
kỷ Ba – Thế kỷ 21 bấp
bênh, du mục – di dân – điện thoại
…
ĐTS: Bài thơ tác giả gửi đến còn rất dài, xem tiếp ở
http://thotanhinhthuc.org/old/THTHTML-N/NHVThoBaiThoTinhLuongTu.php
Làm gì trong Thế giới đang quay cuồng bất định anh ơi ?
=====================
Ngay khi em còn buốt đau
Thế giới vẫn quay cuồng
Ngay giữa lúc mọi điều đều sai hỏng
Ngay cả khi em lạc lõng vong thân mất tong
Thế giới vẫn quay điên cuồng không chờ không đợi .. ..
Thế giới đang quay cuồng bất định ! Em ơi !
* * *
Thời gian không ngừng cánh lại
Dù chỉ chờ rước kiệu em đi .. ..
Mây ngàn năm bay không bao giờ quay lại
Tất cả đổi thay
Tất cả diễn ra
Dù em không muốn vậy bao giờ
Thế giới đang quay cuồng bất định ! Em ơi !
* * *
Tương Lai thay đổi nhanh với nhiều ẩn số
Bao dự đoán trật lất phút cuối không ngờ
Obama không đánh bại Clinton dù chỉ một tiểu bang ! ?
Nay Tổng thống thứ 44 của Hoa Kỳ.
Ai chẳng cả tin việc ổn định hệ thống ngân hàng Hoa Kỳ
Cổ phiếu Citigroup trong một tuần giảm 75% dưới 5 đôla
Ai chẳng cả tin ba công ty sản xuất xe hơi lớn nhất
Nay đang hấp hối từng giờ trên giường bệnh
Như bong bóng chứng khoán công nghệ Thông tin
Hàng loạt ngân hàng hàng đầu phá sản
Thị trường tài chính ngạt thở
Thất nghiệp ngày mỗi tăng
Sản xuất suy sụp
Thế giới không còn như Thời Hoàng kim xưa nữa !
Mô hình siêu tự do đã chấm dứt !
Thế giới đang quay cuồng bất định ! Em ơi !
* * *
Thế giới đang hình thành một trật tự mới
Ngôi làng Toàn cầu nhiều vận hội cũng lắm rủi ro
Gắn bó vô tình vô cơ đan bện vào nhau
Liên kết hữu cơ hữu ý gắn kết lẫn nhau
Hai nước Mỹ-Tàu biện chứng bạn-thù
Như hai anh em song sinh dính chung sườn
Sinh-tử biện chứng cộng sinh
Trạng chết thì Chúa cũng băng hà !
Thế giới hữu cơ đang quay cuồng bất định ! Em ơi !
* * *
Trần gian điên dại này không tự hủy vì lòng căm thù
Mà lại là do lòng tham vô đáy
Trần gian điên dại này không tự hủy vì ngay cả bom nguyên tử tự sát
Mà lại là phương tiện tài chính siêu tự do
Tử thù nước Mỹ không từ bên ngoài
Y nằm ngay giữa trái tim Hoa Kỳ
Nằm ngay trên Phố Tường Nữu Ước
Nối giáo cho kẻ tử thù này là Vua lừa Ma-Đớp (1)
Là các ngài chủ ngân hàng tham lam không đáy
Là các nhà kinh tế Giải Nobel
Sáng tạo ra mô hình kinh tế quái thai đồng lõa
Thay vì hàng trăm ngàn người chết
Là hàng triệu người mất việc làm
Bàng hoàng trước một Thế giới đầy tiềm năng
Bỗng chốc đói nghèo
Thế giới hữu cơ đang quay cuồng bất định ! Em ơi !
* * *
Sẽ ra sao Ngày Mai ?
Và cứ thế Thế giới quay vần
Nhân loại đang lâm nguy trong Khủng hoảng Toàn cầu
Hàng tỷ vì sao lạc giữa Thiên hà
Chiếu dõi hàng tỷ số phận bên dưới
Ngày tháng trôi qua
Sự cố đổi thay
Sự Sống và cái Chết
Như dòng đời yên bình tựa bóng chim Câu
Khi Thế giới quay đúng điệu hòa âm vũ trụ
Thời gian trôi hút tận Không gian .. ..
Thế giới hữu cơ đang quay cuồng bất định ! Em ơi !
* * *
Đừng buồn nữa nghe em !
Điệu buồn xanh đơn
Điệu buồn xanh đơn
Chẳng khác gì hơn
Tiếng đàn bầu tủi hờn
Hãy cười lên đi em trong khoảnh khắc
Lượng tử Thời gian ngắn ngủi
Đừng buồn nữa nghe em !
Điệu buồn xanh đơn
Hãy nghĩ vui lên em !
Đừng buồn
Vui
Em hãy cười ngạo nghễ từ miệng vết thương đau
Cho da non khép lại
Em hãy cười khinh mạn
Cho nước mắt tủi hờn cuốn đi
Nhảy múa luân vũ vào những khắc giây tồi tệ
Vứt đi bỏ đi giọt lệ sầu trần gian nhân thế
Thế giới hữu cơ đang quay cuồng bất định ! Em ơi !
* * *
Em cần Hy vọng: thần dược cho sự sống còn
Đừng hận thù
Đừng tự cô lập mình
Chiến đấu
Không thể thua cuộc
Chấp nhận bao dung
Nhưng không để lạm dụng
Cùng dựa lưng nhau cùng nhau chiến đấu
Thành một chiến hào chung
Tiến lên ! Tiến lên !
Không còn đường lùi
Duy nhất đường ấy sinh tồn
Trong Thế giới hữu cơ đang quay cuồng bất định ! Em ơi !
TỶ LƯƠNG DÂN
1. Bernard Madoff Bẹc-Cà-Na Ma-Đớp , 70 tuổi người Pháp Phú Lăng Sa gốc Do Thái …. sáng lập và TGĐ Thị trường chứng khoán Nasdaq, Thị trường chứng khoán lớn thứ 2 tại Phố Tường – Nữu Ước Wall Street, New York. Bernard Madoff Bẹc-Cà-Na Ma-Đớp bị kết tội lừa đảo gian lận 50 tỉ mỹ kim !
Y vừa nộp phạt 5 triệu mỹ kim (quả là bụi chỉ là 1 phần 50.000 so với số tiền lường đảo 50 tỉ mỹ kim !!! ) để tại ngoại
Em tưởng Max Planck cũng có rất nhiều công trong lý thuyết lượng tử chứ nhỉ.
Em rất hâm mộ Lisa Randall. Anh Sơn có quan điểm gì về lý thuyết của bà này không? Giới vật lý đánh giá bà ấy có cao không?
1.-Lý thuyết lượng tử có hai giai đoạn–lý thuyết lượng tử “cũ” bắt đầu từ Planck, và lý thuyết lượng tử “mới” bắt đầu từ Heisenberg, Schrödinger. 2.-Giới vật lý đánh giá rất cao bà Randall.
Wow, câu hỏi vì sao electron không rơi vào nhân em tự hỏi bao lâu nay mà không trả lời được, :). Cảm ơn anh nhiều.
Thế tại sao mặt trăng lại không rơi vào trái đất nhỉ? Giải thích theo thuyết lượng tử chắc không được rồi. Lúc nào GS có thời gian lại giảng tiếp về vấn đề này được chứ ạ?
Câu hỏi rất hay! Đúng là mặt trăng ở trên quỹ đạo giữ một năng lượng rất lớn, so với mặt trăng rơi xuống trái đất. Thế tại sao nó không rơi xuống và giải phóng ra năng lượng ấy? Câu trả lời rất đơn giản: “cơ chế không cho phép!”
Nhắc lại rằng, năng lượng không tự nhiên sinh ra, và cũng không tự nhiên mất đi; nó chỉ chuyển từ dạng này sang dạng khác. Như vậy năng lượng mà mặt trăng giải phóng ra trong khi nó rơi xuống trái đất phải được biến thành một dạng năng lượng nào khác. Nhưng thành dạng nào? Ma sát là một cơ chế rất quen thuộc để biến động năng thành nhiệt. Nhưng mặt trăng chuyển động trong chân không, nên ma sát không có.
Khi hai chất điểm quay quanh nhau, cơ chế duy nhất để năng lượng thoát đi là thông qua việc phát ra sóng hấp dẫn. Sóng hấp dẫn giống như sóng điện từ, chỉ khác nó là dao động của trường hấp dẫn chứ không phải trường điện từ. Nhưng lực hấp dẫn rất yếu, nên sóng hấp dẫn phát ra cũng rất yếu. Năng lượng thất thoát đi qua sóng hấp dẫn là không đáng kể: công suất chỉ là 10 microwatt đối với mặt trăng, quá nhỏ để gây hiệu ứng đáng kể. Do đó, mặt trăng không rơi xuống trái đất bằng cách phát ra sóng hấp dẫn được.
Quay lại electron chuyển động trong nguyên tử. Do electron mang điện tích, nên theo lý thuyết cổ điển nó phải phát ra sóng điện từ lúc quay xung quanh hạt nhân. Sóng điện từ mạnh hơn nhiều sóng hấp dẫn, electron mất năng lượng rất nhanh, rơi vào hạt nhân trong vòng 10 nanô giây, nếu như không có cơ học lượng tử cứu vãn.
Như hòn đá rơi xuống mặt đất. Mặt trăng rơi xuống trái đất sẽ biến thành động năng. Nghĩa là vận tốc của mặt trăng so với trái đất tăng dần lên.
Nếu giải thích như Sơn nói: mặt trăng ko rơi xuống trái đất vì ko giải phóng được năng lượng bằng cách toả nhiệt. Vậy các thiên thể, các sao chổi vẫn đâm xuống các hành tinh, mặt trời trong khi đang thực hiện quỹ đạo của chúng thì vì cái gì ? ( có rất nhiều trường hợp các thiên thể bay quanh mặt trời theo những quỹ đạo xác định, rồi một ngày kia đài báo đưa tin: vì thiên thể bay quá gần mặt trời – hoặc là hành tinh a,b,c…. – nên bị hút và rơi vào mặt trời – hay hành tinh a,b,c… đó.
Anh Sơn có thể nói thêm vì sao xunglượng lại tính bằng p=h/r không ạ?
Hơn nữa theo cách giải thích ở trên thì có vẻ electron luôn di chuyển trên mặt cầu có bán kính tới hạt nhân là r=h^2/(me^2) cố định. Nhưng trong sách vật lý Toán em học thì thấy hàm sóng của electron có dạng c exp(-ax) với các hằng số c,a, và do đó về mặt nguyên tắc electron có thể xuất hiện ở bất kỳ đâu. Vậy có mâu thuẫn gì không?
Thưa giáo sư Đàm Thanh Sơn, theo em được biết thì công thức p=h/(r*2 pi) là nằm trong giả thiết của Borh Summerfeld và sau đó được tính toán cụ thể dựa vào trị riêng của toán tử moment góc và yêu cầu tính đơn trị của hàm sóng.
Nhưng theo cách giải thích công thức này của giáo sư, em hiểu là giáo sư đánh giá rằng độ bất định của tọa độ chính là đường tròn bán kính r. Và có vẻ là cũng không khác việc đánh giá sự liên hệ bất định giữa moment góc và tọa độ góc.
Xin cảm ơn giáo sư đã cho em cách nhìn mới hơn.
Xin hỏi giáo sư thêm một câu hỏi là theo ý kiến giáo sư, liệu nguyên lý bất định đến một lúc nào đó sẽ có thể sai không?
Các bạn hoadai, Dung Nguyen,
Các công thức trong bài của tôi phần lớn đều chỉ là đánh giá cỡ độ lớn. Đúng ra trong những trường hợp này ta phải dùng dấu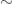 thay cho dấu bằng. Ví dụ công thức tôi viết ở trên,
thay cho dấu bằng. Ví dụ công thức tôi viết ở trên,  , thực ra phải là
, thực ra phải là  , cho phép hai vế lệch nhau vài lần. Đánh giá này bắt nguồn từ hệ thức bất định: Nếu điện tử cách hạt nhân một khoảng cách cỡ bằng
, cho phép hai vế lệch nhau vài lần. Đánh giá này bắt nguồn từ hệ thức bất định: Nếu điện tử cách hạt nhân một khoảng cách cỡ bằng  thì độ bất định của xung lượng của nó phải ít nhất là cỡ
thì độ bất định của xung lượng của nó phải ít nhất là cỡ  . Giả sứ như điện tử ở trạng thái cơ bản, năng lượng ít nhất, thì xung lượng của nó chí ít cũng phải cỡ
. Giả sứ như điện tử ở trạng thái cơ bản, năng lượng ít nhất, thì xung lượng của nó chí ít cũng phải cỡ  , không thì nguyên lý bất định bị vi phạm.
, không thì nguyên lý bất định bị vi phạm.
Tất nhiên trong cơ học lượng tử, ta không nên hình dung ra điện tử chỉ chuyển động trên vòng tròn có một bán kính nhất định. Do đó công thức xác định cũng phải hiểu như một đánh giá cỡ độ lớn:
cũng phải hiểu như một đánh giá cỡ độ lớn: 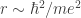 , tức là điện tử ở loanh quanh cỡ khoảng bán kính Bohr, Còn nếu muốn biết chính xác hơn thì phải giải phương trình Schrödinger, và ra hàm sóng
, tức là điện tử ở loanh quanh cỡ khoảng bán kính Bohr, Còn nếu muốn biết chính xác hơn thì phải giải phương trình Schrödinger, và ra hàm sóng  giống như bạn hoadai viết.
giống như bạn hoadai viết.
Cũng có thể dùng quy tắc lượng tử hóa Bohr-Sommerfeld cho nguyên tử hydro. Rất ngẫu nhiên trong trường hợp nguyên tử hyđro quy tắc này cho kết quả chính xác cho các mức năng lượng. Bình thường nó chỉ cho kết quả gần đúng. Điều này có vẻ có nguyên nhân sâu xa, liên quan đến vectơ Laplace-Runge-Lenz và đối xứng SO(4).
Nguyên lý bất định có một vị trí trung tâm trong vật lý lượng tử, tôi không hình dung là nó có thể bị vi phạm như thế nào.
Anh Son co the noi sau hon mot chut ve tinh doi xung SO(4) va vector Laplace-Rung-Lenz de giai thich vi sao quy tac luong tu hoa cua Bohr lai cho ket qua chinh xac khong a?
Mot dieu nua, anh noi nguyen ly bat dinh co vi tri trung tam trong vat ly luong tu; lieu co phai ban chat cua no la tinh hermitian cua cac toan tu. Anh co the binh luan, hoac cho bon em them mot so thong tin ve truong phai non-hermitian quantum mechanics khong a?
Em cam on anh.
P/s: Xin loi vi may cua em khong co bo go tieng Viet nen em khong go chu co dau duoc, mong anh thong cam.
Vấn đề về nguyên lý bất định rất hấp dẫn và em muốn hiểu hơn về lý do nó tồn tại. Em cũng công nhận nó là trung tâm của cơ học lượng tử, nhưng vẫn chưa thật sự hiểu nó một cách tường tận.
Có một số cách thu được hệ thức bất định sử dụng bất đẳng thức Schwarz. Có thể sử dụng tính Hermitian của các toán tử ( Như trong Sakurai) hoặc không cần đến tính Hermitian. Nhưng em thấy là đều đã sử dụng đến các tiên đề về cơ sở, toán tử và kết quả của phép đo đại lượng vật lý. ( Em cũng chưa thấy cách nào cho mix ensemble ). Nhưng em vẫn không tin đây là các cách chứng minh thực sự, vì nếu không thì sẽ phải là hệ thức bất định chứ không phải là nguyên lý bất định.
Em cũng mong chờ giải thích thêm của giáo sư cho câu hỏi bạn Minh Nguyen về tính đối xứng của nhóm SO(4).
Xin cảm ơn giáo sư và mong giáo sư có thêm nhiều bài viết để mơ mang kiến thức. Mặc dù em học vật lý nhưng còn nhiều điều học mà không hiểu chu đáo.
Cảm ơn anh Sơn đã giải thích. Mặc dù cách tính này là dễ hiểu (heuristically) nhưng em vẫn thấy nó chưa chặt chẽ lắm, vì nếu dùng nguyên lý bất định thì chỉ suy ra năng lượng E>= -e^2/r+ h^2(2mr), và số r cực tiểu hóa vế phải (là bán kính Bohr) không hẳn là số r cực tiểu hóa năng lượng E.
Có lẽ ở đây ta đã ngầm giả sử là tại ground state của nguyên tử hydro thì bất đằng thức ở nguyên lý bất định xảy ra gần “=”. Theo cách nhìn này thì có vẻ nguyên lý bất định liên hệ mật thiết với một nguyên lý cơ bản khác là năng lượng không liên tục mà bị phân thành nhiều “gói” quantum, và nói riêng là có 1 mức năng lượng nhỏ nhất (không có mức trung gian từ nó tới 0). Điều này có đúng không ạ?
Minh Nguyen, Dung Nguyen, hoadai,
Rất hân hạnh được tiếp chuyện các bạn. Tôi trả lời ở dưới, có gì không rõ các bạn lại hỏi tiếp.
1. Về vectơ Laplace-Runge-Lenz và đối xứng SO(4) của bài toán Kepler các bạn có thể tìm đọc ở nhiều chỗ. Trong cơ học cổ điển, có thể đọc ở Goldstein, Classical Mechanics. Trong cơ học lượng tử, có thể đọc ở Gottfried and Yau, Quantum Mechanics: Fundamentals. Hay tìm đọc trong Landau and Lifshitz tập 1 và tập 3, nhưng chú ý là trong đó véctơ này không mang tên gì cả. Trên mạng cũng có nhiều tài liệu về vấn đề này, ví dụ ở wikipedia.
2. Véctơ Laplace-Runge-Lenz có liên quan đến sự chính xác của phép lượng tử hóa Bohr-Sommerfeld? Đây là giả thuyết thôi, và tôi cũng đã thấy nhiều người nêu ý kiến này. Nhưng tôi không tìm thấy đâu giải thích chính xác mối liên hệ giữa hai cái này. Bài báo gần với đề tài này nhất tôi tìm thấy là bài này. Nếu làm sáng tỏ được vấn đề này thì tốt quá.
3. Về đánh giá năng lượng trạng thái cơ bản của nguyên tử hydro qua nguyên lý bất định: tất nhiên đây chỉ là đánh giá cỡ độ lớn và không mang tính chặt chẽ toán học. Có thể làm cho nó chặt chẽ hơn, ví dụ dùng variational method, dùng Gaussian wavepacket như là trial wave function (các bạn biết Gaussian wavepacket đạt cực tiểu cho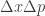 , nếu hiểu
, nếu hiểu  và
và  là root mean square).
là root mean square).
4. Nguyên lý bất định liên quan tới tính không giao hoán của các cặp toán tử ví dụ như ,
,  . Các đại lượng đo được thường đều tương ứng với các toán tử hermit. Rất tiếc tôi không biết gì về cơ học lượng tử không hermit cả.
. Các đại lượng đo được thường đều tương ứng với các toán tử hermit. Rất tiếc tôi không biết gì về cơ học lượng tử không hermit cả.
Chứng minh hệ thức bất định thì người ta hay dùng bất đẳng thức Schwarz (còn gọi là Cauchy-Bunyakovsky). Chứng minh này trong các sách hay viết cho pure state, nhưng có thể mở rộng cho mixed state. Chìa khóa là mệnh đề sau: nếu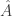 là một toán tử thì giá trị trung bình của
là một toán tử thì giá trị trung bình của  không âm, và trung bình có thể lấy theo pure hay mixed state đều được (sau đó ta xét
không âm, và trung bình có thể lấy theo pure hay mixed state đều được (sau đó ta xét  ).
).
5. Tôi dùng lẫn lộn thuật ngữ “hệ thức bất định” và “nguyên lý bất định”. Cảm giác của tôi là “hệ thức bất định” nhấn mạnh về khía cạnh toán, chính xác, còn “nguyên lý bất định” nhấn mạnh khía cạnh triết học.
Em đọc trong cuốn “Lưới trời ai dệt” của Nguyễn Tường Bách nói là do nguyên lý bất định mà chân không xung quanh chúng ta không phải là” chân không tuyệt đối”, mà có rất nhiều lỗ đen nhỏ li ti, chợt hiện rồi chợt mất (có thuyết nói rằng lỗ đen vốn là hút tất cả mọi thứ, nhưng khi nó quá “đầy” thì nó sẽ nổ tung và trả lại tất cả). Cách nhìn kiểu “vô trung sinh hữu” này rất thú vị, nhưng em không biết có đúng không? (nguyên lý bất định áp dụng cho chân không???)
Tôi không có cuốn sách đó ở đây, nhưng xem một bản trên net thì không thấy chỗ nào tác giả Nguyễn Tường Bách viết như vậy. Bạn có thể xem lại cho chính xác được không?
Còn khái niệm “chân không” trong vật lý hiện đại phức tạp phức tạp hơn khái niệm chân không trong đời sống hàng ngày (chân không = không có gì).
Ta sẽ không xét lực hấp dẫn, vì lý thuyết lượng tử của lực này ta chưa biết. Các lực khác được mô tả bằng lý thuyết trường lượng tử, là sự hợp nhất của cơ học lượng tử và thuyết tương đối hẹp. Trong lý thuyết trường lượng tử
chân không = trạng thái cơ bản
(trạng thái có năng lượng nhỏ nhất của Hamiltonian). Hamiltonian mô tả thế giới của ta (nó được gọi là “mô hình chuẩn”) không phải là đơn giản, nên chân không là một trạng thái phức tạp. Đôi khi người ta tưởng tượng nó như một trạng thái trong đó các cặp hạt-phản hạt liên tục sinh ra và tự hủy đi. Người ta thường viết công thức cho chuyện này: năng lượng
cho chuyện này: năng lượng 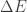 sinh ra và hủy đi trong thời gian
sinh ra và hủy đi trong thời gian  . Ví dụ, một cặp electron- phản electron, có năng lượng
. Ví dụ, một cặp electron- phản electron, có năng lượng 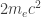 (nhớ lại công thức của Einstein E=mc2) chỉ tồn tại trong thời gian
(nhớ lại công thức của Einstein E=mc2) chỉ tồn tại trong thời gian 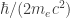 , nhỏ hơn 10-21 giây. Nhưng thực ra, đó chỉ là bức tranh các nhà vật lý sử dụng để giúp việc tưởng tượng ra trạng thái này thôi, còn về thực chất, chân không là trạng thái có năng lượng cực tiểu.
, nhỏ hơn 10-21 giây. Nhưng thực ra, đó chỉ là bức tranh các nhà vật lý sử dụng để giúp việc tưởng tượng ra trạng thái này thôi, còn về thực chất, chân không là trạng thái có năng lượng cực tiểu.
Cảm ơn anh đã giải thích điều này rõ ràng. Em nhớ nhầm, có thể em nhớ từ cuốn “Lược sử thời gian” của Hawking (HỐ ĐEN KHÔNG ĐEN LẮM) http://www.thuvienhoasen.org/luocsuthoigian-07.htm.
Tuy nhiên xem lại thì ở đó cũng nói về sự liên tục xuất hiện hạt và phản hạt (chứ không phải những lỗ đen nhỏ li ti), và xem đó là một cơ chế để lỗ đen bức xạ năng lượng.
Thực ra nếu hạt và phản hạt xuất hiện và biến đi trong chân không, thì lỗ đen về nguyên tắc cũng có thể như vậy. Nhưng ta biết quá ít về vật lý lượng tử của các lỗ đen vi mô (ít nhất là tôi biết quá ít) nên không thể rút ra được bài học gì từ điểm này. Ví dụ ta có thể hỏi lỗ đen có bức xạ ra lỗ đen hay không? Có lẽ trong phần lớn các trường hợp xác suất của quá trình này quá nhỏ so với việc bức xạ ra các hạt bình thường.
Anh Sơn này, cụ Hawking này liệt toàn thân, thậm chí hình như cả đầu cũng nghẹo sang 1 bên, không thể điều khiển được. Thế thì cụ cảm nhận không trọng lượng kiểu gì nhỉ???
http://www.vnexpress.net/GL/Khoa-hoc/2010/04/3BA1B33C/
anh Sơn ơi ở đây em có mấy người có nói về electron chuyển động trong hạt nhân. Hôm trước em có đọc sách Quantum mechanics symmetries của Greiner thấy có đề cập đến chuyển động của electron ở đây còn tiến động trên trục nữa. Và trong đó tác giả có nói về xuất hiện đối xứng động lực. Nhưng khái niệm nó không rõ ràng tí nào. Anh có thể nói cho em hiểu rõ hơn về khái niệm này được không? À mà anh có file ebook nào mà viết về mô hình boson tương tác (IBM)không có thể cho em với. Ở việt nam mình hiếm tài liệu quá. Em là sv năm cuối làm khóa luận mà thiếu tài liệu nên hơi vất vả. Email của em là: nghuuha210@gmail.com.
em cảm ơn anh nhiều nhé. Anh viết về cơ lượng tử rõ quá. chúc anh an lành
hữu hà
Anh trả lời ở đây vì viết công thức dễ hơn.
Đối xứng của một Hamiltonian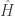 là tập hợp các toán tử
là tập hợp các toán tử  giao hoán với
giao hoán với 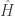 :
: ![[\hat H,\, \hat O]=0](https://s0.wp.com/latex.php?latex=%5B%5Chat+H%2C%5C%2C+%5Chat+O%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) . Các toán tử này lập thành một đại số Lie. Tùy theo
. Các toán tử này lập thành một đại số Lie. Tùy theo 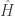 mà đại số Lie này là đại số gì. Ví dụ nếu
mà đại số Lie này là đại số gì. Ví dụ nếu 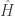 là Hamiltonian của nguyên tử hydro thì đại số này là O(4). Trong vật lý hạt nhân, nếu khối lượng của quark u và d bằng nhau, và bỏ qua tương tác điện từ, thì đại số này là SU(2).
là Hamiltonian của nguyên tử hydro thì đại số này là O(4). Trong vật lý hạt nhân, nếu khối lượng của quark u và d bằng nhau, và bỏ qua tương tác điện từ, thì đại số này là SU(2).
Thưa GS, điều này có thể hiểu là năng lượng của hệ trước và sau khi thực hiện phép biến đổi là không đổi được không ạ?
Chào anh Sơn!
Nghe nói nhiều về anh nhưng chưa được hân hạnh gặp mặt, em đang tìm hiểu về đối xứng động lực, anh có thể gợi ý những tài liệu cần đọc. Cảm ơn anh
Em có một thắc mắc mong anh Sơn giải đáp về vận tốc và thời gian: Em đọc báo thấy viết là nếu một du hành gia trên phi thuyền với vận tốc rất nhanh khi thời gian sẽ chậm lại và khi anh ta quay lại trái đất thì anh ta trẻ hơn so với mọi người trên trái đất. Rõ ràng phi thuyền chuyển động so với trái đất. Câu hỏi của em là làm thế nào để nhận biết được phi thuyền hay trái đất động rất nhanh ạ. Nếu em lấy phi thuyền làm mốc thì trái đất chuyển động rất nhanh so với phi thuyền. Thì có kết quả ngược lại là người trên trái đất sẽ trẻ hơn nhà du hành vũ trụ? Em thấy cái định luật thời gian chôi chậm lại khi vận tốc chuyển động nhanh mù mờ quá vì em chả hiểu vận tốc so với cái gì, thời gian là cái gì? Em mong anh giải đáp cho em được không ạ. Em cảm ơn anh nhiều.
Phi thuyền và trái đất khác nhau ở chỗ phi thuyền chuyển động có gia tốc còn trái đất thì không. Phi thuyền phải đi đến một địa điểm, sau đó quay ngược trở lại, lúc nó quay ngược lại là lúc nó chuyển động có gia tốc, tức là không thẳng đều. Trong khi đó trái đất (bỏ qua chuyển động của nó quanh mặt trời) luôn chuyển động thẳng đều. Em có thể đọc một cuốn sách giáo khoa bất kỳ về thuyết tương đối hẹp (ví dụ Taylor & Wheeler, Spacetime physics). Vấn đề em hỏi được gọi là “nghịch lý hai người sinh đôi” (the twin paradox).
Mong anh giúp em để em có thể hiểu hơn về vật lý lượng tử. Vận tốc, thời gian em còn chả hiểu là cái gì (Vận tốc so với cái gì? thời gian là cái gì?) thì làm sao em hiểu được mấy công thức lượng tử. Bụp bụp 1 đống công thức vận tốc, vị trí, …, không có thế giới quan gì cả làm em khó hiểu quá. Ví dụ như em đọc sách thấy họ cứ viết vận tốc nhanh thì thời gian trôi chậm lại thì vận tốc ở đây so với cái gì làm chuẩn ạ?
Các khái niệm vận tốc, thời gian đều lấy từ vật lý cổ điển. Hiện tại để cho đơn giản ta mới chỉ xét trường hợp các vận tốc nhỏ hơn nhiều vận tốc ánh sáng, có thể bỏ qua các hiệu ứng tương đối tính. Thời gian ở đây hiểu như thời gian tuyệt đối của Newton, còn vận tốc thì là vận tốc so với một hệ quy chiếu chuyển động thẳng đều bất kỳ.
câu hỏi của bạn Minh ở trên làm em thấy một điều khá hay là khi một nhà du hành vũ trụ trên con tàu du hành với vận tốc khá lớn (so sánh được với vận tốc ánh sáng) bay ra khỏi trái đất. Nếu như theo thuyết tương đối hẹp của Einstein thì thời gian trôi chậm lại. Tuy nhiên nếu chúng ta giả sử người này trong suốt quá trình du hành mà không gặp phải trường hấp dẫn nào khác thì theo thuyết tương đối tổng quát thì thời gian của anh ta lại trôi nhanh hơn so với trái đất vì ở trái đất chịu trọng lực.
như vậy nếu chúng ta kết hợp hai thuyết lại thì liệu khi đó có còn nghịch lý anh em sinh đôi nữa không hả anh Sơn.
câu hỏi này em chưa tìm được một đáp án nào cho dễ hiểu anh có thể nói qua cho em được không?
Nếu con tàu chuyển động với vận tốc so sánh được với tốc độ ánh sáng thì thời gian trên đó chắc chắn sẽ chạy chậm hơn thời gian trên trái đất, vì sự chậm lại của đồng hồ do trường hấp dẫn của trái đất là rất yếu.
Định lượng hơn thì là như sau. Đồng hồ trên mặt đất chạy với tốc độ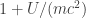 lần đồng hồ ở vô cực, trong đó
lần đồng hồ ở vô cực, trong đó 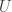 là thế năng của đồng hồ,
là thế năng của đồng hồ, 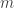 là khối lượng của nó, và
là khối lượng của nó, và  là tốc độ ánh sáng. Nhưng ta biết
là tốc độ ánh sáng. Nhưng ta biết  trong đó
trong đó 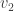 là tốc độ vũ trụ cấp hai,
là tốc độ vũ trụ cấp hai, 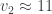 km/s. Như vậy đồng hồ trên trái đất chạy với tốc độ
km/s. Như vậy đồng hồ trên trái đất chạy với tốc độ 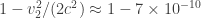 lần đồng hồ ở vô cực.
lần đồng hồ ở vô cực.
Bạn có thể dễ dàng kiểm tra là nếu con tàu chuyển động (ở ngoài bất cứ trường hấp dẫn nào) với tốc độ lớn hơn tốc độ vũ trụ cấp hai, thì thời gian trên con tàu sẽ trôi chậm hơn thời gian trên mặt đất.
Tôi nghe nói là độ chính xác của hệ thống định vị toàn cầu (GPS) đòi hỏi người phải tính đến hiệu ứng của trường hấp dẫn lên thời gian.
(chú thích: tôi mới sửa lại dấu của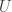 cho đúng).
cho đúng).
Cảm ơn anh Sơn đã giải đáp thắc mắc của em. Em theo Toán nên chỉ biết về cơ học cổ điển thôi ạ. Mặc dù thế giới nguyên tử là rất nhỏ bé nhưng em nghĩ vẫn phải mô tả được nó đúng không ạ? Về câu hỏi trên em vẫn còn một thắc mắc là làm thế nào để nhận biết được hệ quy chiếu đang chuyển động thẳng đều hay công nhận một hệ nào đó chuyển động thẳng đều rồi các hệ khác cứ theo chuẩn của hệ này thôi. Chắc một vật chuyển động thẳng đều thì có thể nhận ra nhờ vào quan sát quá trình chuyển động của từng phần của vật đó với nhau vì khi vật đó thay đổi vận tốc thì bao giờ cũng có một số phần của vật đó thay đổi trước rồi kéo các phần khác của vật đó thay đổi theo tạo ra sự hỗn loạn của các thành phần bên trong vật đó nếu như nó không có sự kết dính vững chắc. Do đó chắc là quan sát quá trình chuyển động các thành phần trong vật đó với nhau thì biết được vật đó có chuyển động thẳng đều hay không. Mọi thành phần của trái đất ổn định với nhau thì chắc trái đất đang chuyển động thẳng đều. Khi giả thiết có lực hấp dẫn vào thì trái đất bị mặt trời hút nên phải chuyển động quanh mặt trời để trái đát không bị rơi vào mặt trời.
Trình độ hiểu biết của em về vật lý còn non lắm ạ. Để mọi người đều có thể hiểu được vật lý lượng tử từ những bài giảng của anh. Mong anh giải thích, mô tả các khái niệm trong toán học, vật lý lượng tử với thế giới vật chất nhiều hơn và có những ví dụ, bài tập liên quan đến thế giới vật chất. Ví dụ như tại sao lại có khái niệm toán tử, …., rồi tích cái này với cái kia. Anh có thể mô tả các khái niệm đó ứng với cái gì trong thế giới vật chất ạ mặc dù chắc là cũng không có điều kiện để quan sát bằng mắt thường vì thế giới lượng tử nhỏ qua. Phép tích đó có giao hoán hay không giao hoán phụ thuộc vào nội dung của phép tích đó chứ ạ. Tự nhiên bụp bụp cái này tích cái kia, cái này là toán tử, cái này là số kia. Em thấy như thế thì thành Toán học mất vì không có liên hệ với thế giới vật chất nữa. Em cảm ơn và biết ơn anh rất nhiều ạ!
Cái này chắc khó em ạ. Không thể giảng bài qua blog được. Em phải đọc sách thôi. Cơ học lượng tử thì cuốn D. Griffiths, Introduction to Quantum Mechanics có lẽ là dễ đọc nhất lúc nhập môn.
Hôm rồi em ngồi học mạch op-amp thì thấy có một điểm này, các hệ thống ổn định chống nhiễu thì nó đòi hỏi hệ thống phải có hồi tiếp, sự hồi tiếp này đưa đến kết quả là nó tạo ra một giới hạn giữa độ lợi áp và băng thông nôm na là :
A*f <= Hằng số. Trong đó A là độ lợi áp và F là băng thông.
Điều này làm em liên tưởng đến nguyên lý bất định của Heisenberg. Liệu vũ trụ là một chu trình khép kín ?
Chẳng hạn,nếu lấy sự sống trên trái đất làm minh họa thì rõ ràng, nó cũng là một chu trình tuần hoàn. Vậy là chu trình tuần hoàn có phải là một nguyên lý phổ quát không nhỉ . Nếu thế thì từ nguyên lý bất định Heisenberg, có cái gì đang tuần hoàn diễn ra không ? Rất mong anh Sơn hé mở cho một vài bí mật 🙂
Tôi dốt về mạch điện lắm nên không thể comment về cái này. Có duration-bandwidth relationship có vẻ giống nguyên lý bất định nhất.
Nguyên lý bất định của Heisenberg cũng như nguyên lý loại trừ Pauli đều là những nền tảng của cơ học lượng tử.
Nếu không có nguyên lý Heisenberg thì chưa chắc đã có cuộc tranh cãi nảy lửa ở những năm 30 của thế kỷ trước, và được gói gọn ở 3 từ EPR ( Einstein- Podolsky – Rosen). Sau này, Bohm và cậu học trò Aharnov (1957) đã giải quyết một nửa vấn đề liên quan đến thí nghiệm ảo EPR, Bell (1964) cùng một loại thí nghiệm sau đó đã giải quyết nửa còn lại của nghịch lý EPR.
Nguyên lý ngoài trừ Pauli có ảnh hưởng cũng rất lớn, từ cấp độ hạ nguyên tử, liên kết hóa học ( giải thích vì sao lại xây dựng được bảng Tuần hóa các nguyên tố hóa học), đến các phản ứng xảy ra trong quá trình sụp đổ của sao lùn trắng. Nguyên lý loại trừ Pauli liên quan đến các hạt có spin bán nguyên ( như electron), và từ đó dẫn đến một loạt lý thuyết, cũng như ứng dụng chỉ xoay quanh hai vấn đề fermions và bosons, hàm sóng đối xứng và hàm sóng phi đối xứng.
Thuyết bất định có vẻ giống thuyết không thể biết trong triết học?
Thuyết không thể biết là agnosticism? Nếu thế thì nguyên lý bất định không phải như vậy. Ngược lại, quan điểm trường phái Copenhagen là cơ học lượng tử cho ta thông tin toàn vẹn về hệ vật lý bất kỳ ta nghiên cứu. Không bao giờ x và p cùng được xác định, không phải là do ta không biết được, mà do bản chất của sự vật là như vậy.
Ngày nào em cũng dạo qua blog của giáo sư mà vẫn chưa có bài viết mới. Mong giáo sư có thời gian rảnh để viết thêm về đề tài này. Khi em học về nguyên lý bất định, em đọc được rằng x và p không thể đo được đồng thời và được giải thích dựa trên mô hình về tọa độ và xung lượng của một hàm sóng. Rồi sau đó là chứng minh bằng đại số của nguyên lý bất định như trong sách về cơ học lượng tử. Thế nhưng tự thấy bản thân còn dốt nên vẫn thấy mình chưa hiểu nguyên nhân của nguyên lý bất định cũng như bản chất đằng sau của nó. Một vấn đề nữa cũng khiến em không yên ổn là nguyên lý Pauli. Đến giờ em vẫn không thoải mái mỗi lần chấp nhận nó. Mong có dịp được giáo sư khai trí.
Cám ơn bạn đã dùng nguyên lý bất định để giải thích tại sao electron lại ko bị hút vào hạt nhân. Mình đọc và nảy ra một câu hỏi là: có thể dùng nguyên lý bất định để giải thích nguyên nhân tại sao mặc dù trái đất và mặt trăng hút lẫn nhau nhưng tại sao mặt trăng chỉ quay xung quanh trái đất mà ko bị hút vào không ? Xin chỉ ra tính toán cụ thể.
Bạn xem https://damtson.wordpress.com/2010/04/15/uncertainty-principle/#comment-57 và câu trả lời.
Pingback: Nghịch lý Einstein – Podolsky – Rosen (EPR Paradox ) « Vatlyvietnam's Blog
<<<>>>>>
Tôi có thể help anh Sơn để giải thích một cách đơn giản cho bạn như sau.
Xét A là một đại số giao hoán với phép nhân . . Bây giờ, ta tìm cách nào đó deform phép nhân ấy đi, thay vì a.b ta thay bằng a*_t b thỏa mã a*_0b=a.b
Khi đó, ta có một họ các đại số phụ thuộc vào một tham số t mà khi t=0 nó chính là đại số giao hoán ban đầu. Ta yêu cầu a*_tb- b*_ta=t.{a,b}
Nói một cách đơn giản, thuần túy toán học, đây là một curve trên không gian moduli các cấu trúc đại số xuất phát từ một đại số giao hoán theo hướng của cấu trúc Poisson. Chú ý, có rất nhiều điều kiện để có thể deform như vậy, và chúng được thể hiện thông qua đối đồng điều Holdchild và deformation theory.
Ta áp dụng kỹ thuật trên vào đại số các hàm trên T*M, phân thớ đối tiếp xúc của một đa tạp M, và ta thu được đại số giao hoán các phép đo của một hệ vật lý. Bây giờ, khi ta biến dạng nó đi từ a.b thành a*_t b thì cái tích đó không còn giao hoán nữa, nhưng vẫn còn kết hợp.
Vì vậy ta thay a bởi toán tử l_a, biến l_a(b) thành a*_t b thì ta sẽ thu được một biểu diễn của đại số A_t này lên trên chính nó. Trong nhiều truờng hợp, ta có thể polarize đại số này bằng một nửa số chiều (tôi không muốn giải thích số chiều Gelfand-Kirilov) và thu được một không gian Hilbert (skip a lot of detail).
Hệ quả, đại số các phép đo trên một hệ cơ học cổ điển bị biến dạng thành một đại số các toán tử trên không gian Hilbert. Chơi game với để thu được các kết quả của cơ học cổ điển là một vấn đề rất dễ dàng.
hì bài viết của G.S hay quá ,em cũng đang là sv năm thứ 3 , em chưa hiểu hết cái hay của vật lý ,hôm nay học về nguyên lý bất định ,nhờ đọc bài viết của GS mà em hiểu hơn ,cảm ơn G.S ạ
chúc GS ngày vui vẻ nhé ^^
Anh Son oi, anh co the giang cho bon em nghe mot chut’ ve Wilson operator duoc khong a?
Wilson operator là gì?
Nguyên lý bất ổn của Heissenberg hoặc Schrodinger còn mang nặng tính duy ý chí! Điện tử vùng vẫy đánh phá nhà tù. Thế giới ngầm Dirac cũng vậy. Đó là cơ chế xin cho mập mờ! Thật không hổ thẹn khi theo nghề toán. Hoàn toàn định tính được hệ động lực mà không cần một cơ chế mập mờ nào cả! Các bạn trẻ có thấy đáng tự hào vì Lịch sử đã trao cho mình một sứ mệnh thiêng liêng không?
Sao chổi thì lao vào trái đất còn mặt trăng thì bay quanh trái đất và điện tử cũng bay quanh hạt nhân? Vì sao nào? Các bạn trẻ có biết định tính phương trình vi phân và quỹ đạo tuần hoàn của trường véc tơ không? Tuỳ theo khối lượng khoảng cách kích thước và vận tốc ban đầmà ta có 3 quỹ đạo: Tuần hoàn (mặt trăng trái đất), hội tụ (lao vào tâm như sao chổi quá nhẹ) và tựa tuần hoàn (điện tử bay quanh hạt nhân theo quỹ đạo tựa tròn)
Vì không quan tâm đến lý thuyết định tính hệ động lực nên mẫu hành tinh nguyên tử không sát với thực nghiệm. Các vì sao có kích thước không lồ khối lượng riêng lại rất lớn nên chúng bay theo quỹ đạo tuần hoàn. Sao chổi nhẹ quá nên mới lao vào trái đất. Điện tử có kích thước nhỏ còn hạt nhân có khối lượng riêng rất lớn nên bay theo quỹ đạo tựa tròn. Bán kính Bohr là giới hạn mà điện tử có thể tiếp cận mà không bao giờ đạt tới.
Con lắc đồng hồ cũng vậy. Nếu vận tốc ban đầu vừa phải nó sẽ dao động quanh trục đứng. Còn nếu bạn đánh mạnh quá nó sẽ bay xung quanh cái đồng hồ. Nếu bạn dùng súng AK mà nã đạn thì nó sẽ vỡ tan thôi. Xin chân tình giới thiệu với các bạn trẻ hiếu học Lý thuyết định tính phương trình vi phân và hệ động lực vô cùng hấp dẫn và có cả ứng dụng trong thị trường tài chính kinh tế vĩ mô? Vì sao kinh tế thế giới cứ bị khủng hoảng nhỉ? Thời ông cha chúng mình đã bị, đến thời mình rồi mà vẫn không tránh được?
Vì sao kinh tế Việt Nam cứ trì trệ kém phát triển nhỉ? Người Việt nam thì chăm chỉ làm ăn mà vẫn không giàu nhỉ? Hệ động lực và phương trình vi phân có thể dụ báo được hết! Nhưng không chạm tự ái của mọi người trong cộng đồng được. Đành tâm sự với các bạn trẻ là học, học nữa, học mãi! Sinh ra là để học mà? Các bạn sẽ tìm thấy thiên đường toán học thôi!
Thực ra tín đồ mộ đạo chưa tìm thấy cuốn sách nào hay về hệ động lực cả. Đành gửi gắm tin yêu vào các bạn trẻ Việt Nam hy sinh quên mình mà viết ra cuốn kinh Thiên Cổ Hùng Văn cho toàn thế giới ngưỡng mộ! Thực vây không một nơi nào trên bầu trời trên mặt đất hay trong lòng đất mà lại không có hệ động lực. Hệ Động Lực thật là vô cùng hấp dẫn. Vi mô (nguyên tử hạt nhân) vĩ mô (sao trăng) dân số, sinh học, tài chính. Thế mà chưa có cuốn kinh nào thật sự Thánh Kinh cho hệ động lực? Cũng chưa bao giờ có cuốn Thánh Kinh cho toàn dân ta xây dựng đất nước mạnh giàu! Toàn là những sách nửa vời, duy ý chí.
Chao ơi, chủ nghĩa xã hội là gì mà toàn dân ta phải chiến đấu phải hy sinh để bảo vệ, phải lao động nhọc nhằn để xây dựng? Các bạn trẻ có quan tâm đến hệ động lực dân số không? Có bạn nào trả lời cho tôi không?
Em cũng chỉ là dân amateur về vật lý thôi, thấy rằng thắc mắc của bạn “phuong” ở trên có vẻ chưa được trả lời thỏa đáng.
và
Xin được có ý kiến giải thích thế này:
Trái đất và mặt trăng đủ lớn để áp dụng cơ học Newton. Trạng thái cân bằng mặt trăng quay quanh trái đất (mà không rơi xuống) là vì hợp lực tác động lên mặt trăng bằng 0. (ở đây tính 2 lực lớn là lực hấp dẫn và lực ly tâm do chuyển động tròn gây ra, 2 lực này bằng nhau).
Nếu không có gì thay đổi thì hệ thống mãi cân bằng như vậy. Nhưng ta đang bàn đến “Nguyên lý bất định” nên không có hệ thống nào là không thay đổi. Anh Sơn đã giải thích sự mất mát “nội động lực” đầu tiên của mặt trăng do ma sát là bằng 0, mất mát thứ 2 do sóng hấp dẫn là rất bé nên để dẫn đến mất cân bằng động toàn hệ thống sẽ là rất lâu dài… đến mức mình không cảm nhận thấy được.
Tuy nhiên các yếu tố trên chưa phải là tổng lực tác động vào hệ thống cân bằng này, còn bao nhiêu thứ khác: lực hấp dẫn từ mặt trời, từ các vì sao khác, bức xạ từ mặt trời,… <= tất cả sẽ ảnh hưởng đến cân bằng động này. Vì vậy có lẽ ý của bạn "phuong" là làm sao chứng minh cân bằng động (việc mặt trăng quay quanh trái đất) là một cân bằng bền ?
Cảm ơn anh rất nhiều vì bài viết, xin được vào blog của anh để đọc hết tất cả (hôm nay e mới biết blog này, vì vô tình tìm hiểu xem độ bất định về vận tốc tối thiểu là bao nhiêu thì mới có thể xác định đồng thời cả vận tốc và tọa độ). Cảm ơn anh!
1. Cơ học lượng tử và vật lý vũ trụ là những vấn đề khá hóc búa và trừu tường. Nó nằm cảm giác thông thường, muốn cảm nhận được phải có trí tưởng tượng phong phú và tư duy toán học nhất định. Tôi thấy trong blog này nhiều bạn thắc mắc khi chưa thật sự tìm hiểu các kiến thức cơ bản.
2. Về câu hỏi phi thuyền và trái đất tôi thấy anh Sơn chưa trả lời hợp lý. Ý người hỏi là khi phi thuyền chuyển động so với Trái đất thì ngược lại Trái đất cũng chuyển động đối với phi thuyền. Theo thuyết tương đối mọi hệ quy chiếu đều có vai trò như nhau, có nghĩa là ta không thể coi trái đất đứng yên và phi thuyền chuyển động được. Như thế tại sao người trên Trái đất lại già nhanh hơn, tại sao không ngược lại hoặc giống nhau?
3. Có 1 vấn đề tôi cứ thắc mắc mãi, mong được anh Sơn giúp đỡ, đó là cơ sở của nguyên lý bất định. Chúng ta không thể xác định được chính xác đồng thời vận tốc và vị trí của 1 vật là do công cụ đo của chúng ta (ánh sáng). Tại sao từ đó người ta có thể khẳng định bản chất của vật là bất định được. Điều này cũng như 1 người mù dùng gậy mảnh bằng cao su để xác định vị trí các vật trong nhà. Do tính chất công cụ (gậy) nên ông ta chỉ có thể xác định được vị trí các vật một cách tương đối với sai số nhất định. Ông ta không xác định được chính xác vị trí của vật không có nghĩa là vật phải bất định theo sai số đó. Mong anh giải thích.
Để trả lời câu hỏi thứ 2 của bạn Nguyễn Công Chức ở trên, vận tốc của phi thuyền và trái đất không hoàn toàn giống hệt nhau mà phải có một sự khác biệt giữa chúng. Chính sự khác biệt này khiến cho hai anh em sinh đôi (mà một ở lại trái đất, một bám theo phi thuyền) có tuổi già khác nhau.
Trong trường hợp hai du thuyền chuyển động tương đối (với vận tốc
cố định và chiều hướng đều đặn thẳng) thì hai anh em sinh đôi trên hai du thuyền đó không chút khác biệt gì về tuổi tác.
Phạm Xuân Yêm 27/04/2012
@Nguyen Cong Chuc: Em nghĩ vật lý chỉ khảo sát cái gì “đo” được thôi ạ. Muốn biết tọa độ, xung lượng chỉ có cách là “đo”. Mà trong cơ học cơ học lượng tử, tác dụng của phép đo lên hệ “luôn luôn” không thể bỏ qua được nên ta có nguyên lý bất định. Trong ví dụ của bác, nếu người mù không còn cách nào khác ngoài dùng gậy cao su thì vật lý của người mù này chắc chắn phải chấp nhận nguyên lý bất định.
Giáo sư khi nào có thời gian, có thể viết về cảm giác lâng lâng mà giáo sư cảm nhận được, nhiều điều thú vị cơ học lượng tử liên quan đến cuộc sống thường nhật cho em được hiểu rõ về ý nghĩa và cảm nhận về cơ học lượng tử. Chân thành cảm ơn giáo sư.
Các bạn nên tìm đọc hồi ký của Heisenberg để hiểu thật rõ về ý nghĩa của hệ thức bất định. Hệ thức bất định có thể chứng minh chặt chẽ bằng toán học với mỗi cặp toán tử không giao hoán, mà hệ thức giao hoán của chúng cho một số. Hệ thức này thường gọi là hệ thức lượng tử. Cần phải vạch rõ vai trò của Toán học và Vật lý ở đây. Nếu thừa nhận [x,p] = xp-px= ih, thì hệ thức bất định của Heisenberg chỉ là một phép tính rất nhỏ. Nhưng nhận ra được tọa độ và xung lượng phải là các toán tử thỏa mãn hệ thức lượng tử, thì hoàn toàn độc lập với Toán học. Đặc biệt cống hiến của Heisenberg còn ở việc biểu diễn toán tử p bằng đạo hàm theo x.
Tôi nhớ Niels Bohr đã có giải thích về lý do electron không thể rơi vào hạt nhân không cần dùng tới hệ thức bất định. Cách dùng hệ thức bất định của GS Sơn chỉ giải thích việc không giam được electron vào trong hạt nhân, chứ đúng là không giải thích được vì sao, electron không “rơi” (đến gần hạt nhân hơn mức năng lượng cơ bản của nguyên tử).
Cảm ơn GS Sơn về bài giảng vô cùng trong sáng và dễ hiểu!
cảm ơn GS đã cho e một cách nhìn trực quan về hệ thức bất định và cũng giải thích được tại sao điện tử không rơi vào hạt nhân.
e cũng được đọc qua tài liệu http://iop.vast.ac.vn/~nvthanh/cours/phys/Physics_II_ch8.pdf và cho e hỏi GS : tại sao hệ thức bất định người ta lại biểu diễn được dưới 2 dạng ∆x.∆p≈h và ∆x.∆p≈ℏ , khi nào cần xài cái nào trong trường hợp nào ? và e cũng chả biết từ đâu mà người ta đưa ra hệ thức bất đinh liên hệ năng lượng và thời gian ( chứ không như hệ thức bất định theo tọa độ và động lượng ta có thể đưa ra thí nghiệm nhiễu xạ ánh sáng để chứng minh được ∆x.∆p≈ℏ )
Và có thể cho e hỏi ngu ngoài lề xíu, cái này e không hiểu, tại sao trong biểu thức nặng lượng nguyên tử hidro trong mẫu nguyên tử Bo ta viết được biểu thức E=-(k^2 me^4)/(2n^2 h^2 )=-Rhc/n^2 =-13,6/n^2 (eV) (với c là tốc độ ánh sáng, R là hằng số Ritbe ) điều e muốn hỏi là tại sao lúc rút gọn hằng số Ritbe sao vẫn còn thừa số h.c trên tử mà sao người ta không đưa nó luôn vào hằng số R, phải chăng nó còn ý nghĩa sử dụng nào khác không, mong GS chỉ bảo cho e
Khi nào GS rảnh thì trả lời cho e cũng được ạ, e xin chân thành cám ơn.
Kính gửi Giáo sư Đàm Thanh Sơn
Sau khi đọc bài viết của Giáo sư em đã hiểu thêm về nguyên lý bất định. Em nhận ra rằng nguyên lý này là bản chất của vũ trụ, nó chi phối mọi sự vật, hiện tượng. Chính từ bài tập của Giáo sư em đã hiểu rằng mọi vật chất luôn luôn phải vận động vì nếu đứng yên tức là vận tốc xác định sẽ vi phạm nguyên lý bất định.
Giáo sư cho em hỏi, Vật lý cũng chính là Toán học không. Vì em thấy tất cả các lý thuyết Vật lý đều được mô tả bằng Toán học. Thậm chí nhiều lý thuyết còn dùng Toán học tiên đoán trước mà sau này thực nghiệm xác là đúng. Như vậy có phải Vũ trụ vận động theo các quy luật của Toán học không. Em rất mong Giáo sư giải thích giúp em.
Em xin chúc Giáo sư luôn mạnh khỏe và gặp nhiều may mắn.
Em xin giải bài tập của Giáo Sư
Gọi:
m là khối lượng của hạt neutron (coi như không đổi khi chuyển động);
∆x là độ cao mà hạt neutron phải chuyển động theo Nguyên lý bất định. Đây cũng chính là độ bất định về tọa độ;
v là vận tốc của hạt (với giả thiết hạt chuyển động thẳng đều theo phương thẳng đứng – Như vậy ở đây coi như vận tốc là xác định rồi, không biết có vi phạm Nguyên lý bất định không? Nhờ Giáo sư chỉ giúp em);
g là gia tốc trọng trường của Trái đất nơi đặt hạt, coi như g = 981cm/s^2.
Như vậy, khi hạt chuyển động lên phía trên sẽ sinh ra động năng Wđ = (m.v^2)/2. đến một độ cao bằng ∆x thì hạt sẽ có một thế năng Wt = m.g.∆x. Khi động năng Wđ bằng thế năng Wt thì hạt sẽ dừng lại và rơi xuống.
Vậy ta có: (m.v^2)/2 = m.g.∆x Suy ra: v = (2.∆x.g)^(1/2)
Theo Nguyên lý bất định ta có: ∆x. ∆p = ∆x. ∆[m.(2.∆x.g)^(1/2)] ≥ h/2π
Suy ra ∆x = [(h/2π)^2/(2.m.g)]^(1/3)
Thay các số vào ta được: ∆x = 6,93177 . 10^(-12) cm
Rất mong khi nào Giáo sư có thời gian rảnh rỗi chỉ bảo giúp em và phản hồi của những người quan tâm khác.
Em xin chân thành cảm ơn.
Giáo sư cũng cho em hỏi thêm một chút là: Tại sao vận tốc ánh sáng c là cố định không phụ thuộc vào việc chọn hệ quy chiếu đo, cả thuyết tương đối của Einstein và cả thực nghiệm đều xác nhận như vậy.
Em xin cảm ơn Giáo sư.
Cảm ơn bài viết rất đơn giản và dễ hiểu , rất hay
Thưa Giáo sư, tôi đọc trên một blog Phật giáo có đề cập đến Nguyên lý Bất định này và Nguyên lý Bất toàn. Họ so sánh hai Nguyên lý này với ý niệm Vô thường – Vô ngã. Giáo sư thấy họ so sánh có đúng không ạ??? Cám ơn GS rất nhiều.