Trò chơi ghép hình này đơn giản hơn Trí Uẩn, chỉ có 4 mảnh. Có thể ghép 4 mảnh này thành hình vuông
Nhưng bốn mảnh này có thể ghép lại thành hình tam giác đều:
Đố: tìm kích thước của các mảnh (tỷ lệ các cạnh, giá trị của các góc).
Khoa học máy tính- An error has occurred; the feed is probably down. Try again later.
- Vuhavan’s blog
- Bắc Kinh, thủ đô bất đắc dĩ
- World Cup 2022
- Ngày hội toán học (2): Số nguyên tố và giải thưởng Fields
- Lý thuyết cầu hôn hay Lấy người mình yêu và không bỏ được, tập 2.
- Toán học giữa đời thường II: Anh Paul bạch tuộc và luật số lớn
- Đạo văn
- Dạy và học toán I: Cả nhà đều béo
- Tướng Tàu
- Tiến sỹ (tây ta)
- Tiến sĩ (tây tây và ta tây)
- Sổ tay Thích Học Toán
- Bếp rùa
- ZetaMu
- An error has occurred; the feed is probably down. Try again later.
- Le Minh Khai
- On Being Southeast Asian and the Bankruptcy of Liberal Persuasion
- Chang’an News from Vietnam
- Vietnamese Poetry 4.0
- Moving Forward in the Era of the Decline of Area Studies & the Humanities
- Vietnamese Prehistory and International Scholarship – Part 3: Sauer, Solheim & Hòa Bình
- Agrarian Transformation in Thailand, and Rural-Urban Interactions
- Vietnamese Prehistory and International Scholarship – Part 2: Thought & Solheim
- Vietnamese Prehistory and International Scholarship – Part 1: Introduction
- Tiền sử Việt Nam và học thuật quốc tế (phần 1)
- How May I Help You?
- Hà Huy Khoái
- Alta’s blog
- An error has occurred; the feed is probably down. Try again later.
Dam Thanh Son's Blog 
Sau khi tính toán chi tiết thì em cho rằng là cách xếp này chỉ gần chính xác chứ không chính xác hoàn toàn.![b=\frac{{2a}}{{\sqrt[4]{3}}}](https://s0.wp.com/latex.php?latex=b%3D%5Cfrac%7B%7B2a%7D%7D%7B%7B%5Csqrt%5B4%5D%7B3%7D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![\frac{a}{{\sqrt[4]{3}}}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Ba%7D%7B%7B%5Csqrt%5B4%5D%7B3%7D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Bằng một số lý luận em nhận thấy rằng :
Nếu cạnh của hình vuông là a
Cạnh của tam giác đều là :
Ba góc nhọn ở trong hình vuông là 60 độ.
Cạnh của tam giác vuông nhỏ bằng một nửa cạnh của tam giác đều và bằng:
Đường chéo của tam giác vuông nhỏ cắt một cạnh của hình vuông tại trung điểm M. Hai nét cắt còn lại trong hình vuông cũng có độ dài bằng một nửa cạnh của tam giác đều. Một trong hai nét cắt này cũng cắt cạnh hình vuông tại trung điểm N đối diện với trung điểm M. Nối 2 giao điểm của 2 nét cắt với cạnh của hình vuông ta cũng được một tam giác vuông nhỏ đối diện với tam giác vuông nhỏ trong hình với kích thước giống hệt.
Đến lúc mọi thứ đã sẵn sàng để dựng hình, em check lại thì thấy là đường cao của tam giác đều có cạnh bằng b/2 cộng với 2 lần đường cao hạ từ đỉnh góc vuông của tam giác vuông nhỏ không bằng đường chéo hình vuông ( sai khác ở số thứ 3 sau dấu phẩy). Và em kết luận rằng ta chỉ xếp được tam giác cân gần đều .
Em có một lỗi là việc check sự liên quan các đường cao và đường chéo của hình vuông là lại là không đúng. Vẫn dựng được chính xác hình tam giác. Trong comment trên của em thì “cạnh của tam giác vuông nhỏ bằng một nửa cạnh tam giác đều ” đổi thành “đường chéo của tam giác vuông nhỏ bằng một nửa cạnh của tam giác đều”. Từ kết quả trên có thể tính được là tam giác vuông nhỏ có cạnh là a/2 và
, hai cạnh còn lại thì bằng một nửa cạnh của tam giác đều và bằng: ![\frac{a}{{\sqrt[4]{3}}}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Ba%7D%7B%7B%5Csqrt%5B4%5D%7B3%7D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
, các cạnh của 2 hình tứ giác còn lại có thể tính từ các cạnh của tam giác vuông nhỏ và hình tứ giác góc trên bên trái.
Hình tứ giác phía trên bên trái có 2 cạnh kề với góc vuông có độ dài lần lượt là
a/2 và
Các góc thì ngoài 3 góc nhọn trong hình vuông bằng 60 độ , thì các góc còn lại đều lẻ. Hai góc nhọn của tam giác vuông nhỏ một góc bằng 41 độ, một góc bằng 49 độ. Với giá trị vô tỷ của các cạnh, em nghĩ bài này chắc không thể cắt chỉ với thước và compa.
Em xin lấy lại 1 số kết quả ở trên của bạn Dũng nguyên và sửa lại 1 số chỗ .
Thứ 1 : b=2.a.3^(-1/4)
Thứ 2 : theo hình 1 tứ giác nằm ở trên phía bên trái có diện tích bằng diện tích của tam giác vuông ở dưới phía bên phải + diện tích của tam giác đều có cạnh bằng b/2
Thứ 3: theo hình 1 ta có thể chứng minh dễ dàng giao điểm của các vết cắt là trung điểm cạnh huyền của tam giác vuông phía dưới bên phải.
Thứ 4: Theo hình 1 ta nối điểm cắt ở cạnh trên nối với 2 điểm cắt 2 cạnh bên của hình vuông. Từ điểm cắt ở cạnh bên bên trái ta tiếp tục nối với lại điểm cắt ở cạnh đáy hình vuông.
Từ hình vẽ suy luận ta sẽ có được 4 tam giác vuông ở 4 góc với 2 tam giác vuông có góc vuông đối diện nhau thông qua đường chéo hình vuông là bằng nhau.
Ta lại tiếp tục suy ra tiếp 2 tam giác vuông ở cùng phía bên trái hoặc bên phải là các tam giác vuông đồng dạng với nhau với tỉ lệ diện tích là
Diện tích hình vuông bây giờ là bằng diện tích hình chữ nhật cộng với lại 4 diện tích tam giác vuông ở 4 góc.
Sau 1 hồi tính toán em tính ra được diện tích của tam giác vuông nhỏ theo hình 1 bằng (a^2)/7
Từ đó ta sẽ tính ra được 2 cạnh bên của nó bằng hệ 2 phương trình
c.d=2/7 . (a^2) (*)
c^2 + d^2 = (b^2)/4 = (a^2) / 3^(1/2) (**)
với d = a. (56/98)^(1/2) / 3^(1/4)
với c = a. (2/7). (98/56)^(1/2) . 3^(1/4)
hoặc
với d= a. (42/98)^(1/2) / 3^(1/4)
với c = a. (2/7). (98/42)^(1/2) . 3^(1/4)
tất cả đều cho ra gần bằng 1 cạnh = 0.497a và cạnh kia là 0.574a
từ đây ta suy ra được góc lun 😀
Mình không đọc đoạn tính số nhưng mình cho rằng cái Thứ 3 của bạn không được hợp lý. Vì tam giác vuông nhỏ không cân. Cạnh còn lại của tam giác đều nhỏ song song và bằng cạnh huyền của tam giác vuông nhỏ. Đường cao của tam giác đều nhỏ hạ từ giao điểm của 3 đường cắt sẽ tới trung điểm của cạnh còn lại đó. Tuy nhiên vì tam giác vuông nhỏ không cân, nên giao điểm 3 đường cắt đó không nằm ở trung điểm cạnh huyền tam giác vuông nhỏ được.
Cái hình ở giữa sau khi nối các giao điểm với cạnh của hình vuông cũng thiếu chút xíu nữa là thành hình chữ nhật, vì tam giác vuông nhỏ không cân.
Tuy nhiên mình cũng nói thật là mình chưa nghĩ ra cách cắt nếu không dùng số gần đúng vì mấy cạnh đều là số vô tỷ.
ko đâu , tại vì tứ diện ở trên bên trái, cái bự nhất áh nó bằng chính tam giác vuông nhỏ ở dưới + tam giác đều có cạnh b/2. Khi đó bạn sẽ xét 2 tứ giác bên cạnh cái tứ giác bự ở giữa, bạn sẽ thấy 3 trên 4 cạnh của của mỗi tứ giác đó bằng nhau. Có góc 90 và 60 tương ứng nhau nên buộc cạnh thứ 4 còn lại phải bằng nhau nên nó mới là trung điểm cạnh huyền của tam giác vuông nhỏ ở dưới góc phải đấy chứ ^^.
Còn ở hình 1 nếu bạn nối các giao điểm lại thì cũng có 1 hình chữ nhật hoàn chỉnh đấy, diện tích của nó bằng 2 lần diện tích của tam giác đều nhỏ cạnh b/2. Từ đó suy ra hình 2 ở dưới bạn cũng sẽ có 1 hình chữ nhật luôn chứ ko phải gần bằng đâu ^^. Có điều diện tích của nó lại bằng 4 tam giác vuông nhỏ ở 4 góc ở hình 1.
Ko bạn nói đúng đấy nó ko phải trung điểm thật. Mà sao lạ ta 2 tứ giác ở 2 bên đó có 3/4 cạnh bằng nhau, có 2 góc tương ứng bằng nhau mà lại ko bằng nhau ta.Hay nhỉ.
Mà cũng thật sự phi lý tại theo hình 2 thì cạnh huyền của tam giác nhỏ phải bằng 1 nửa của tam giác đều cạnh b tức nó cũng phải bằng cạnh huyền của tam giác vuông nhỏ ở góc trái phía trên. Như vậy theo hình 1 thì 2 thằng đó phải song song với nhau chứ ta. Tại nếu nó ko song song thì làm sao có được 3 góc 60 độ được. mà có 3 góc 60 độ mà với 2 cạnh huyền song song bằng nhau thế thì bắt buộc nó vẫn phải là trung điểm ở cạnh huyền tam giác vuông dưới ko thể nào khác được. Để có gì mình suy nghĩ thêm.
Hài thật comment liên tục :)) , mình vẫn bảo lưu kết quả trên là đúng 2 hình tứ diện ở 2 bên đó có diện tích bằng nhau :D. Mình xem lại kỹ rùi, nếu để chứng minh giao điểm cắt ở hình 1 là trung điểm của cạnh huyền nhỏ bằng 2 tứ diện 2 bên là ko chính xác phải bằng suy luận ở comment thứ 2 của mình áh. 😀
Cách dựng của mình thế này, mình lấy 2 trung điểm 2 cạnh đối diện của hình vuông, từ đó mình vẽ được 2 cạnh huyền của 2 tam giác vuông nhỏ song song với nhau. ( Cái chỗ này thì mình cheat, vì dùng máy tính để tính căn bậc 4 và dùng thước kẻ có chia vạch để đo rất “nắn nót” ). Lấy trung điểm của một trong 2 cạnh huyền, hạ một đường cao từ đó xuống cạnh huyền kia. Cũng không khó lắm để chứng minh các góc nhọn lúc này bằng 60 độ. ( Mình tìm ra nó sau khi phát hiện lỗi sai của mình ở comment đầu tiên). Cuối cùng là dùng kéo cắt và ghép. Hình của mình chắc là đẹp hơn của giáo sư Sơn vì mình cắt rất cẩn thận ^^( Just kidding).
Ừa ^^, hồi đầu mình cũng thử cắt 1 cái để xem tính ngẫu nhiên của nó, khi sắp thành tam giác đều thì nó có 1 lỗ bự ở giữa cho nên mình nghĩ cần phải tính toán chính xác mới có thể ra được hình như mong muốn. Ban đầu thì mình nghĩ tính góc trước do thấy nó dễ ai ngờ các phương trình là 1 vòng tròn khép kín nên ko ra, quay lại tìm cạnh :D.
Khúc trên em có ghi thiếu, các tam giác vuông có tỉ đồng dạng là 3/4
Bai toan nay trong khong gian ba chieu la mot bai toan rat noi tieng, mot trong 23 bai toan cua Hilbert.
Đây là 1 bài toán nổi tiếng vậy sao ạh. Vậy chắc nó phải có 1 kỹ thuật tính phải nói rất chính xác và phức tạp mà em chưa đủ kiến thức để hiểu. Tại em nghĩ nếu mình chứng minh 3 chiều thì bây giờ mình cũng sẽ nhìn từ trên xuống hay từ hình 3 chiều mình sẽ chiếu nó xuống 1 mặt 2 chiều, tìm cái 2 chiều được thì cái 3 chiều sẽ tìm ra được, cách suy nghĩ quả là khá đơn giản nên chắc ko đúng so với 1 bài toán nổi tiếng như vậy ^^.
Cách chia hình vuông để xếp được hình tam giác đều này thường được cho là do Dudeney nghĩ ra đầu tiên năm 1902. Nhưng theo cuốn Frederickson, Hinged dissections: swinging & twisting thì người đầu tiên nghĩ ra có thể là người khác.
Các bạn xem video: Dudeney’s dissection
cách làm của em như hình vẽ:
A, C là trung điểm của hình vuông; A,B là trung điểm tam giác
-> kích thước các mảnh đã rõ
Có thể dựng bằng thước và compa, vấn đề chỉ là dựng điểm B sao cho AB = 1/2 cạnh tam giác, tức là![AB =\frac{{2a}}{{\sqrt[4]{3}}}](https://s0.wp.com/latex.php?latex=AB+%3D%5Cfrac%7B%7B2a%7D%7D%7B%7B%5Csqrt%5B4%5D%7B3%7D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
với a là cạnh hình vuông. Cái này đơn giản khi sử dụng hệ thức trong tam giác vuông, và tam giác đều.
dựng đoạn AB:
Giáo sư cho em hỏi tuy có hơi ngớ ngẩn nhưng em muốn biết : ông Dudeney nghĩ ra mấy câu đố này để chi vậy ạh như cái hình vẽ mà giáo sư đưa ra trong blog này đó ạh.
Tôi đoán là để cho vui thôi. Ông này là tác giả của vô cùng nhiều câu đố khác nhau. Câu đố của ông ta nguyên là: cắt tam giác đều thành một số mảnh nhỏ nhất để có thể gép thành hình vuông. Câu đố này được đăng trên báo; phần lớn các lời giải gửi đến đều là 5 mảnh. Riêng một độc giả gửi đến lời giải với 4 mảnh.
Mình chưa thử dựng bằng thước và compa, nhưng mình không tin có thể dựng được căn bậc 4 của 3. Liên hệ giữa các cạnh của một hình đều liên quan đến khoảng cách giữa các điểm, và theo mình thì các phương trình đều là bậc 2. Nên mình nghĩ là chỉ dựng được canh căn bậc 2 thôi. Nếu chỉ dùng các liên hệ trong tam giác thì các liên hệ này sẽ gói gọn trong định lý hàm số cos. Và mình tin là với cách này , dựng căn bậc 3 hay căn bậc 4 đều không làm được.
Xin lỗi, mình đã sai, vẫn có thể dựng được như sau: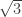
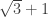
![\sqrt {{{\left( {\sqrt 3 + 1} \right)}^2} - {2^2}} = \sqrt 2 \sqrt[4]{3}](https://s0.wp.com/latex.php?latex=%5Csqrt+%7B%7B%7B%5Cleft%28+%7B%5Csqrt+3++%2B+1%7D+%5Cright%29%7D%5E2%7D+-+%7B2%5E2%7D%7D++%3D+%5Csqrt+2+%5Csqrt%5B4%5D%7B3%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![\sqrt[4]{3}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B3%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Ta dựng được
thì có thể dựng được
và dựng được
và cuối cùng là
Mình xem cách dựng của bạn thì thấy hay hơn nhiều.
Từ các kết quả mình chứng minh được có thể dựng được
![a.\sqrt[{{2^n}}]{x}](https://s0.wp.com/latex.php?latex=a.%5Csqrt%5B%7B%7B2%5En%7D%7D%5D%7Bx%7D&bg=ffffff&fg=333333&s=0&c=20201002)
và
với mọi giá trị của
Bằng thước và compa. Tuy nhiên mình vẫn chưa nghĩ ra cách dựng các căn khác của
Mình dùng tính chất của số nguyên tố và chứng minh được chặt chẽ là không dựng được các căn khác của x bằng các liên hệ là phương trình bậc 2.
Bài toán dựng hình mà bạn Dũng Nguyễn nói là một bài toán cổ điển trong lí thuyết Galois về cách dựng hình bằng thước và compass. Kết quả của bạn là chính xác.
Thưa giáo sư cho em hỏi bài toán mà giáo sư Vũ Hà Văn nhắc tới có phải về nghịch lý Banach-Tarski không ạ ?
Tôi đoán là GS Vũ Hà Văn định nói đến bài toán thứ 3 của Hilbert: http://en.wikipedia.org/wiki/Hilbert%27s_third_problem